类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．
（1）概念理解
如图1，在四边形ABCD中，添加一个条件使得四边形ABCD是“等邻边四边形”．请写出你添加的一个条件．
（2）问题探究
①小红猜想：对角线互相平分的“等邻边四边形”是菱形．她的猜想正确吗？请说明理由。
②如图2，小红画了一个Rt△ABC，其中∠ABC=90°，AB=2，BC=1，并将Rt△ABC沿∠ABC的平分线BB＇方向平移得到△A＇B＇C＇，连结AA＇，BC＇．小红要是平移后的四边形ABC＇A＇是“等邻边四边形”，应平移多少距离（即线段BB＇的长）？
（3）应用拓展
如图3，“等邻边四边形”ABCD中，AB=AD，∠BAD+∠BCD==90°，AC，BD为对角线，AC=
AB．试探究BC，CD，BD的数量关系．
义洁中学计划从荣威公司购买A、B两种型号的小黑板，经洽谈，购买一块A型小黑板比买一块B型小黑板多用20元．且购买5块A型小黑板和4块B型小黑板共需820元．
（1）求购买一块A型小黑板、一块B型小黑板各需要多少元？
（2）根据义洁中学实际情况，需从荣威公司购买A、B两种型号的小黑板共60块，要求购买A、B两种型号小黑板的总费用不超过5240元．并且购买A型小黑板的数量应大于购买A、B种型号小黑板总数量的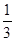
．请你通过计算，求出义洁中学从荣威公司购买A、B两种型号的小黑板有哪几种方案？
“五一”假期，黔西南州某公司组织部分员工分别到甲、乙、丙、丁四地考察，公司按定额购买了前往各地的车票，如图所示是用来制作完整的车票种类和相应数量的条形统计图，根据统计图回答下列问题：
（1）若去丁地的车票占全部车票的10%，请求出去丁地的车票数量，并补全统计图（如图所示）．
（2）若公司采用随机抽取的方式发车票，小胡先从所有的车票中随机抽取一张（所有车票的形状、大小、质地完全相同、均匀），那么员工小胡抽到去甲地的车票的概率是多少？
（3）若有一张车票，小王和小李都想去，决定采取摸球的方式确定，具体规则：“每人从不透明袋子中摸出分别标有1、2、3、4的四个球中摸出一球（球除数字不同外完全相同），并放回让另一人摸，若小王摸得的数字比小李的小，车票给小王，否则给小李．”试用列表法或画树状图的方法分析这个规则对双方是否公平？
如图，AB是⊙O的直径，弦CD⊥AB与点E，点P在⊙O上，∠1=∠C，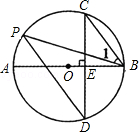
（1）求证：CB∥PD；
（2）若BC=3，sin∠P=
，求⊙O的直径．
（1）计算：
．
（2）先化简，再求值：
，其中
．
已知抛物线y1=ax2+bx+c（a≠0）的顶点坐标是（1，4），它与直线y2=x+1的一个交点的横坐标为2．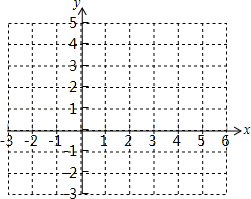
（1）求抛物线的解析式；
（2）在给出的坐标系中画出抛物线y1=ax2+bx+c（a≠0）及直线y2=x+1的图象，并根据图象，直接写出使得y1≥y2的x的取值范围；
（3）设抛物线与x轴的右边交点为A，过点A作x轴的垂线，交直线y2=x+1于点B，点P在抛物线上，当S△PAB≤6时，求点P的横坐标x的取值范围．