（本题12分）一商场对每天进店人数和商品销售件数进行了统计对比，得到如下表格：
人数 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
件数 |
4 |
7 |
12 |
15 |
20 |
23 |
27 |
其中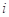
＝1,2,3,4,5, 6,7．
（1）以每天进店人数为横轴，每天商品销售件数为纵轴，画出散点图；
（2）求回归直线方程；（结果四舍五入后保留到小数点后两位）
（3）预测进店人数为80人时，商品销售的件数．（结果保留整数）
（参考公式：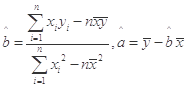
）
（本小题满分14分）设函数
，已知函数
在
处有极值．
(Ⅰ)求实数
的值；
(Ⅱ)当
（其中
是自然对数的底数）时，证明：
；
(Ⅲ)证明：对任意的
，不等式
恒成立．
（本小题满分14分）已知函数
为实常数）．
(I)当
时，求函数
在
上的最小值；
(Ⅱ)若方程
（其中
）在区间
上有解，求实数
的取值范围；
(Ⅲ)证明：
（参考数据：
）
本小题满分14分
正方形
的边长为1，分别取边
的中点
，连结
，
以为折痕，折叠这个正方形，使点
重合于一点
，得到一
个四面体，如下图所示。
 |
（1）求证：
；
（2）求证：平面
。
.(本题14分)
如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD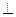
底面ABCD，PD=DC，
E是PC的中点，作EF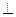PB交PB于点F。
（1）证明：PA//平面EDB；
（2）证明：PB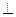平面EFD。
 |
一个几何体的三视图如图所示（单位长度为：cm）：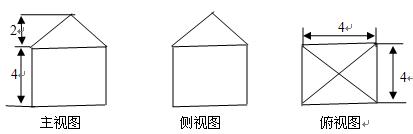
主视图侧视图俯视图
（1）求该几何体的体积；
（2）求该几何题的表面积。