(本题14分)小明在学习平行线相关知识时总结了如下结论:端点分别在两条平行线上的所有线段中,垂直于平行线的线段最短.
小明应用这个结论进行了下列探索活动和问题解决.
问题1:如图1,在Rt△ABC中,∠C=90°,AC=4,BC=3,P为AC边上的一动点,以PB,PA为边构造
□APBQ,求对角线PQ的最小值及PQ最小时 的值.
的值.
(1)在解决这个问题时,小明构造出了如图2的辅助线,则PQ的最小值为 ,当PQ最小时 = _____ __;
= _____ __;
(2)小明对问题1做了简单的变式思考.如图3,P为AB边上的一动点,延长PA到点E,使AE=nPA(n
为大于0的常数).以PE,PC为边作□PCQE,试求对角线PQ长的最小值,并求PQ最小时 的值;
的值;
问题2:在四边形ABCD中,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3.
(1)如图4,若 为
为 上任意一点,以
上任意一点,以 ,
, 为边作□
为边作□ .试求对角线
.试求对角线 长的最小值和PQ最小时
长的最小值和PQ最小时 的值.
的值.
(2)若 为
为 上任意一点,延长
上任意一点,延长 到
到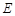 ,使
,使 ,再以
,再以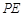 ,
, 为边作□
为边作□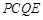 .请直接写出对角线
.请直接写出对角线 长的最小值和PQ最小时
长的最小值和PQ最小时 的值.
的值.
某商店先在广州以每件15元的价格购进某种商品10件,后来又到深圳以每件12.5元的价格购进同一种商品40件.如果商店销售这些商品时,每件定价为x元,可获得大于12%的利润,用不等式表示问题中的不等关系,并检验x=14(元)是否使不等式成立?
根据不等式的性质,把下列不等式表示为x>a或x<a的形式:
(1)10x-1>9x;(2)2x+2<3;(3)5-6x≥2
有5支排球劲旅A队、B队、C队、D队、E队,参加排球锦标赛,成绩如下:D队的名次比C队低,A队比B队高,但低于E队;E队比C低,B队比D队高,请问:这5支球队各是第几名。解决这类问题,一个非常方便的方法是利用数学符号帮忙,此处用“>”或“<”,将成绩可简单表示成不等式,很快就得出这5个队的名次,试一下吧?
比较下面每小题中两个算式结果的大小(在横线上填“>”、“<”或“=”).
(1)32+422×3×4;(2)22+222×2×2;(3)12+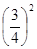 2×1×
2×1×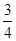 ;
;
(4)(-2) 2+522×(-2)×5;(5)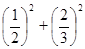
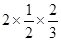 .
.
通过观察上面的算式,请你用字母来表示上面算式中反映的一般规律.
班级50名学生上体育课,老师出了一道题目:现在我拿来一些篮球,如果每5人一组玩一个篮球,有些同学没有球玩;如果每6人一组玩一个篮球,就会有一组玩篮球的人数不足6个.你们知道有几个篮球吗?
甲同学说:如果有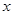 个篮球,
个篮球,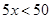 .
.
乙同学说: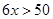 .
.
丙同学说: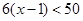 .
.
你明白他们的意思吗?