已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.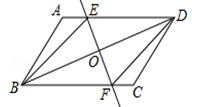
(1)求证:OE=OF.
(2)当∠DOE等于 度时,四边形BFDE为菱形.(直接填写答案即可)
(本小题满分10分)如图,直线AB与坐标轴分别交于点A、点B,且OA、OB的长分别为方程x2-6x+8=0的两个根(OA<OB),点C在y轴上,且OA︰AC=1:2,D(3,0)直线CD垂直于直线AB于点P,交x轴于点D。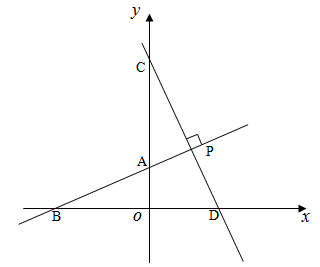
(1)求出点A、点B的坐标。
(2)请求出直线CD的解析式。
(3)若点M为坐标平面内任意一点,在直线AB上是否存在这样的点M,使以点B、D、M为顶点的三角形与△AOB相似,若存在,请直接写出点M的坐标;若不存在,请说明理由。
去年牡丹江管理局西瓜喜获丰收,瓜农老李收获的200吨西瓜计划采用批发和零售两种方式进行销售。经市场调查发现:批发销售每吨可获利200元,零售每吨可获利600元。
(1)若老李计划将这200吨西瓜批发销售x吨,其余零售,设所获总利润y元,试写出y与x之间的函数
关系式。(不必写出自变量的取值范围)
(2)如果老李决定将这200吨西瓜采取批发和零售两种销售方式,他预计获利不低于50000元,不高于52000元。请问共有几种销售方案?(批发和零售的吨数均为正整数)
(3)老李决定将(2)中获利的20﹪全部用来购进今年种植西瓜所需的A、B两种化肥,其中A种化肥每吨4000元,B种化肥每吨2000元(A、B两种化肥的吨数均为正整数)。请直接写出老李有哪几种购进方案.
(本小题满分8分)在△ABC中,AB=AC,CG⊥BA交BA的延长线于点G.一等腰直角三角尺按如图1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边在一条直线上,另一条直角边恰好经过点B.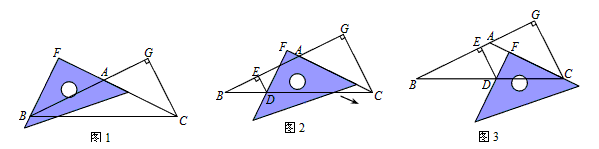
(1)在图1中请你通过观察、测量BF与CG的长度,猜想并写出BF与CG满足的数量关系,然后证明你的猜想;
(2)当三角尺沿AC方向平移到图2所示的位置时,一条直角边仍与AC边在同一直线上,另一条直角边交BC边于点D,过点D作DE⊥BA于点E.此时请你通过观察、测量DE、DF与CG 的长度,猜想并写出DE+DF与CG之间满足的数量关系,然后证明你的猜想;
(3)当三角尺在(2)的基础上沿AC方向继续平移到图3所示的位置(点F在线段AC上,且点F与点C不重合)时,(2)中的猜想是否仍然成立?(不用说明理由)
B岛位于自然环境优美的西沙群岛,盛产多种鱼类。A港、B岛、C港依次在同一条直线上,一渔船从A港出发经由B岛向C港航行,航行2小时时发现鱼群,于是渔船匀速缓慢向B港方向前行打渔。在渔船出发一小时后,一艘快艇由C港出发,经由B岛前往A港运送物资。当快艇到达B岛时渔船恰好打渔结束,渔船又以原速经由B岛到达C港。下面是两船距B港的距离y(海里)与渔船航行时间x(小时)的函数图象,结合图象回答下列问题:
(1)请直接写出m,a的值.
(2)求出线段MN的解析式,并写出自变量的取值范围。
(3)从渔船出发后第几小时两船相距10海里?
牡丹江管理局大力开展“阳光体育”活动,某校利用大课间举办阳光体育竞赛.下图为该校八年1班2014年参加竞赛比赛(包括跳绳、踢毽、排球、篮球四个类别)的参赛人数统计图: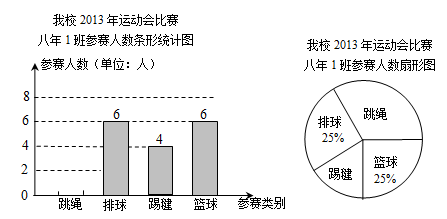
(1)该班参加踢毽、篮球比赛的人数分别是人和人;
(2)该班参加运动会比赛的总人数是人,跳绳所在扇形的圆心角的度数是°,
并把条形统计图补充完整;
(3)从全校参加运动会比赛选手中随机抽取80人,其中有32人获奖. 今年该校中小学参加运动会比赛人数共有1485人,请你估算今年参加运动会比赛的获奖人数大约是多少人?