（本小题14分）如图，二次函数y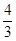x2bxc的图象与x轴交于A-优题课

（本小题14分）如图，二次函数y=x²+bx+c的图象与x轴交于A（3，0），B（﹣1，0），与y轴交于点C．若点P，Q同时从A点出发，都以每秒1个单位长度的速度分别沿AB，AC边运动，其中一点到达端点时，另一点也随之停止运动．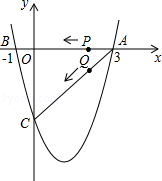

（1）求该二次函数的解析式及点C的坐标；
（2）当点P运动到B点时，点Q停止运动，这时，在x轴上是否存在点E，使得以A，E，Q为顶点的三角形为等腰三角形？若存在，请求出E点坐标；若不存在，请说明理由．
（3）当P，Q运动到t秒时，△APQ沿PQ翻折，点A恰好落在抛物线上D点处，请判定此时四边形APDQ的形状，并求出D点坐标．
（4）在AC段的抛物线上有一点R到直线AC的距离最大，请直接写出点R的坐标．

科目数学题型解答题难度较难

知识点：二次函数在给定区间上的最值

如图，在平面直角坐标系 $xOy$ 中，一次函数 $y ＝ ax + b （ a \neq 0 ）$ 的图象与反比例函数 $y = \frac{k}{x} （ k \neq 0 ， x ＞ 0 ）$ 的图象相交于 $A （ 1 ， 5 ）$ ， $B （ m ， 1 ）$ 两点，与x轴，y轴分别交于点C，D，连接OA，OB．

（1）求反比例函数 $y = \frac{k}{x} （ k \neq 0 ， x ＞ 0 ）$ 和一次函数 $y ＝ ax + b （ a \neq 0 ）$ 的表达式；

（2）求 $△ AOB$ 的面积．

某学校组织了以“纪念革命先烈，激发爱国热情”为主题的爱国主义教育研学活动，参加活动的学生可从学校提供的四个研学地点中任选一个，地点如下：

A：陇南市宕昌县哈达铺红军长征纪念馆；

B：陇南市两当兵变纪念馆；

C：甘南州迭部县腊子口战役纪念馆；

D：张掖市高台县中国工农红军西路军纪念馆．

小宁和小丽决定通过抽签的方式确定本次研学活动目的地，请你用树状图或列表的方法求出小宁和小丽抽到同一地点的概率．

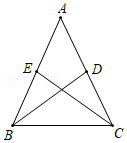
如图，在 $△ ABC$ 中， $AB ＝ AC$ ，点D，E分别是AC和AB的中点．求证： $BD ＝ CE$ ．

如图，在直角坐标系中，四边形 $OABC$ 是平行四边形，经过 $A (- 2, 0)$ ， $B$ ， $C$ 三点的抛物线 $y = a x^{2} + bx + \frac{8}{3} (a < 0)$ 与 $x$ 轴的另一个交点为 $D$ ，其顶点为 $M$ ，对称轴与 $x$ 轴交于点 $E$ ．

（1）求这条抛物线对应的函数表达式；

（2）已知 $R$ 是抛物线上的点，使得 $ΔADR$ 的面积是 $▱ OABC$ 的面积的 $\frac{3}{4}$ ，求点 $R$ 的坐标；

（3）已知 $P$ 是抛物线对称轴上的点，满足在直线 $MD$ 上存在唯一的点 $Q$ ，使得 $∠ PQE = 45 °$ ，求点 $P$ 的坐标．

如图， $ΔABC$ 内接于 $⊙ O$ ， $AD$ 平分 $∠ BAC$ 交 $BC$ 边于点 $E$ ，交 $⊙ O$ 于点 $D$ ，过点 $A$ 作 $AF ⊥ BC$ 于点 $F$ ，设 $⊙ O$ 的半径为 $R$ ， $AF = h$ ．

（1）过点 $D$ 作直线 $MN / / BC$ ，求证： $MN$ 是 $⊙ O$ 的切线；

（2）求证： $AB \cdot AC = 2 R \cdot h$ ；

（3）设 $∠ BAC = 2 α$ ，求 $\frac{AB + AC}{AD}$ 的值（用含 $α$ 的代数式表示）．

试卷网试题网古诗词网作文网范文网