如图甲所示,带斜面的足够长木板P,质量M=3kg.静止在水平地面上,其右侧靠竖直墙壁,倾斜面BC与水平面AB的夹角、两者平滑对接。t=Os时,质量m=1kg、可视为质点的滑块Q从顶点C由静止开始下滑,图乙所示为Q在O~6s内的速率随时间t变化的部分图线。已知P与Q间的动摩擦因数是P与地面间的动摩擦因数的5倍,sin370=0.6,cos370=O.8,g取10m/s2。求:
(1)木板P与地面间的动摩擦因数。
(2)t=8s时,木板P与滑块Q的速度大小。
如下图所示,让摆球从图中的C位置由静止开始摆下,摆到最低点D处,摆线刚好被拉断,小球在粗糙的水平面上由D点向左做匀减速运动,到达A孔进入半径R=0.3m的竖直放置的光滑圆弧轨道,当摆球进入圆轨道立即关闭A孔。已知摆线长L=2m,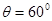 ,小球质量为m=0.5kg,D点与小孔A的水平距离s=2m,g取10m/s2。试求:
,小球质量为m=0.5kg,D点与小孔A的水平距离s=2m,g取10m/s2。试求:
(1)求摆线能承受的最大拉力为多大?
(2)要使摆球能进入圆轨道并且不脱离轨道,求粗糙水平面摩擦因数μ的范围。
某娱乐场所欲建一大型娱乐设施,为论证其可行性,专家评委对所规划的项目先进行理想化分析,若该设施关键部分可简化为模型如图所示,光滑水平面AB与竖直面内的半圆形光滑导轨在B点相切,半圆形导轨的半径R为5m.一个质量为10kg的物体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右的速度后脱离弹簧,当它经过B点进入导轨之后沿导轨向上运动,恰能到达最高点C.(不计空气阻力,AB间足够长)试求: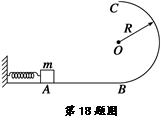
物体在A点时弹簧的弹性势能。
(2)物体到达B点时对轨道的压力的大小。
如图所示,在距地面H=0.8m高的水平桌面上,固定一个末端切线水平的粗糙曲面。一质量为0.2kg的小球自曲面上某点由静止释放,已知该点到桌面的高度h=0.5m,小球落地点到桌子边缘的水平距离s=1.2m,则小球在曲面上运动过程中克服摩擦力所做的功。(g取10m/s2)
一汽车的质量为4000kg,在平直公路上行驶,发动机额定功率120kw,汽车所受阻力为车重的0.2倍,g取10m/s2求
(1)汽车的最大行驶速度。
(2)若汽车由静止开始,以0.5m/s2 的加速度匀加速行驶,这一过程能维持多长时间。
已知某行星的半径为R,行星表面重力加速度为g,不考虑行星自转的影响。若有一卫星绕该行星做匀速圆周运动,运行轨道距行星表面高度为h,求卫星的运行周期T。