如图,在由边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.
(1)将△ABC绕点A顺时针旋转90°,画出相应的△AB1C1;
(2)将△AB1C1沿射线AA1平移到△A1B2C2处,画出△A1B2C2;
如图,BD=CD,BF⊥AC于F,CE⊥AB于E。求证:点D在∠BAC的角平分线上。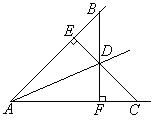
如图所示,AE是∠BAC的角平分线,EB⊥AB于B,EC⊥AC于C,D是AE上一点,求证:BD=CD。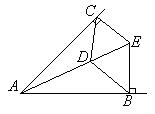
如图:AD=EB, BF=DG, BF∥DG,点A、B、C、D、E在同一直线上。求证: AF=EG。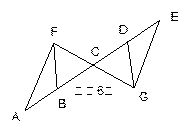
如图,已知∠1=∠2,∠3=∠4,AB与CD相等吗?请你说明理由. 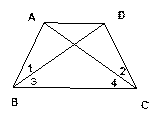
(本题满分12分)
已知点C为线段AB上一点, 分别以AC、BC为边在线段AB同侧作△ACD和△BCE, 且CA=CD, CB=CE, ∠ACD=∠BCE, 直线AE与BD交于点F.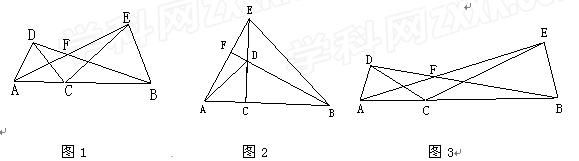
(1)如图1,求证:△ACE≌△DCB。
(2)如图1, 若∠ACD=60°, 则∠AFB= ;
如图2, 若∠ACD=90°, 则∠AFB= ;
(3)如图3, 若∠ACD=β, 则∠AFB= (用含β的式子表示)
并说明理由。