已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连结BD.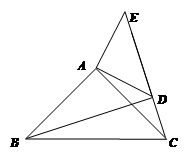
求证:(1)△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.
如图,⊙ 的半径为6,线段
的半径为6,线段 与⊙
与⊙ 相交于点
相交于点 、
、 ,
, ,
, ,
, 与⊙
与⊙ 相交于点
相交于点 ,设
,设 ,
, .
.
(1)求 长;
长;
(2)求 关于
关于 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;
(3)当 ⊥
⊥ 时,求
时,求 的长.
的长.
如图,直线 与
与 轴、
轴、 轴分别相交于点
轴分别相交于点 、
、 .抛物线
.抛物线 与
与 轴的正半轴相交于点
轴的正半轴相交于点 ,与这个一次函数的图像相交于
,与这个一次函数的图像相交于 、
、 ,且
,且 .
.
(1)求点 、
、 、
、 的坐标;
的坐标;
(2)如果 ,求抛物线
,求抛物线 的解析式.
的解析式.
如图,在△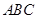 中,
中,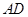 平分∠
平分∠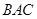 ,
,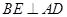 ,
,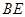 交
交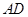 的延长线于点
的延长线于点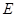 ,点
,点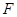 在
在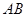 上,且
上,且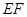 ∥
∥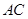 。求证:点
。求证:点 是
是 的中点.
的中点.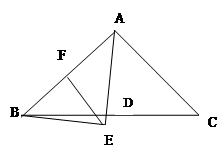
某校为了解全校3200名学生对课外活动体育活动体育项目喜爱程度,就“我最喜爱的课外活动体育项目”从足球、篮球、乒乓球、羽毛球和其它五个类别对部分学生进行了抽样调查(每位同学仅选一项),并根据调查结果制作了不完整的频数分布表和条形图:
| 类别 |
频数 (最喜爱人数) |
频率 |
| 足球 |
 |
0.26 |
| 篮球 |
0.37 |
|
| 乒乓球 |
 |
|
| 羽毛球 |
 |
|
| 其它 |
0.05 |

根据以上图表中提供的信息,回答下列问题:
(1)本次共抽样调查了 名学生;
(2)图表中 = ,
= , = ,
= , = ;
= ;
(3)根据本次抽样调查,试估计该校3200名学生中“最喜爱篮球项目”的学生有多少人?
如图,在平行四边形 中,
中, ,
, ,
, ,垂足为
,垂足为 ,
, .
.
(1)求 、
、 的长;
的长;
(2)求 的正切值.
的正切值.