已知数轴上点A与点B的距离为16个单位长度，点A在原点的左侧，到原点的距离为26个单位长度，点B在点A的右侧，点C表示的数与点B表示的数互为相反数，动点P从A出发，以每秒1个单位的速度向终点C移动，设移动时间为t秒．
（1）点A表示的数为 ，点B表示的数为 ，点C表示的数为 ．
（2）用含t的代数式表示P到点A和点C的距离： PA= ，PC= ．
（3）当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动， Q点到达C点后，再立即以同样的速度返回，运动到终点A．
①在点Q向点C运动过程中，能否追上点P?若能，请求出点Q运动几秒追上．
②在点Q开始运动后，P、Q两点之间的距离能否为2个单位？如果能，请求出此时点P表示的数；如果不能，请说明理由．
先化简，再求值：
，其中a，b满足
=0．
（1）计算：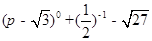
－tan30°
（2）解方程：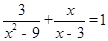
；
（3）解不等式组
，并把解集在数轴上表示出来．
直线
与x轴、y轴分别交于A、B两点，点E从B点出发，以每秒1个单位长度的速度沿线段BO向O点移动（不考虑点E与B、O两点重合的情况），过点E作EF∥AB，交x轴于点F，将四边形ABEF沿直线EF折叠后，与点A对应的点记作点C，与点B对应的点记作点D，得到四边形CDEF，设点E的运动时间为t秒．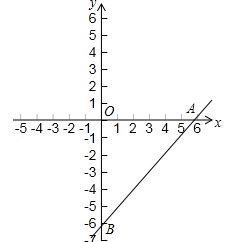
（1）画出当t=2时，四边形ABEF沿直线EF折叠后的四边形CDEF（不写画法）；
（2）在点E运动过程中，CD交x轴于点G，交y轴于点H，试探究t为何值时，△CGF的面积为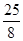
；
（3）设四边形CDEF落在第一象限内的图形面积为S，求S关于t的函数解析式，并求出S的最大值．
某地区为了鼓励市民节约用水，计划实行生活用水按阶梯式水价计费，每月用水量不超过10吨（含10吨）时，每吨按基础价收费；每月用水量超过10吨时，超过的部分每吨按调节价收费．例如，第一个月用水16吨，需交水费17.8元，第二个月用水20吨，需交水费23元．
（1）求每吨水的基础价和调节价；
（2）设每月用水量为n吨，应交水费为m元，写出m与n之间的函数解析式；
（3）若某月用水12吨，应交水费多少元？
如图，已知直线l与⊙O相离．OA⊥l于点A，交⊙O于点P，OA=5，AB与⊙O相切于点B，BP的延长线交直线l于点C．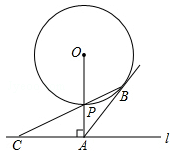
（1）求证：AB=AC；
（2）若PC=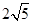
，求⊙O的半径．