（本小题满分9分）如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（1, 0）、C（3, 0）、D（3, 4）．以A为顶点的抛物线y＝ax2＋bx＋c过点C．动点P从点A出发，以每秒
个单位的速度沿线段AD向点D运动，运动时间为t秒．过点P作PE⊥x轴交抛物线于点M，交AC于点N．
（1）直接写出点A的坐标，并求出抛物线的解析式；
（2）当t为何值时，△ACM的面积最大？最大值为多少？
（3）点Q从点C出发，以每秒1个单位的速度沿线段CD向点D运动，当t为何值时，在线段PE上存在点H，使以C、Q、N、H为顶点的四边形为菱形？
比较下列各数的大小关系：
（1）
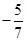和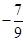
（2）
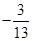，－0．2，－0． 22三个数之间的大小关系
阅读下面解题过程：
计算：
解：
＝
①
＝
②
＝
③
回答：
（1）上面解题过程中有两处错误，第一处是第 步，错因是
，第二处是 ，错因是 ．
（2）正确结果应是 ．
如图为人民公园中的荷花池，现要测量此荷花池两旁A、B两棵树间的距离（我们不能直接量得）．请你根据所学知识，以卷尺和测角仪为测量工具设计一种测量方案．
要求：（1）画出你设计的测量平面图；
（2）简述测量方法，并写出测量的数据（长度用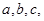
…表示；角度用
…表示）；
（3）根据你测量的数据，计算A、B两棵树间的距离．
如图，在△ABC中，D为BC上一点，∠BAD=∠ABC，∠ADC=∠ACD，若∠BAC=63°，试求∠DAC、∠ADC的度数．
如图，E、F分别为线段AC上两个动点，且DE⊥AC于E，BF⊥AC于F，若AB=CD，AF=CE，BD交AC于M．说明：MB=MD，ME=MF．