如图，边长为1的正方形ABCD一边AD在x负半轴上，直线l：
经过点B（x，1）与x轴，y轴分别交于点H，F，抛物线
顶点E在直线l上．
（1）求A，D两点的坐标及抛物线经过A，D两点时的解析式；
（2）当抛物线的顶点E（m，n）在直线l上运动时，连接EA，ED，试求△EAD的面积S与m之间的函数解析式，并写出m的取值范围；
（3）设抛物线与y轴交于G点，当抛物线顶点E在直线l上运动时，以A，C，E，G为顶点的四边形能否成为平行四边形？若能，求出E点坐标；若不能，请说明理由．
（本题7分）
（1）当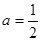
，
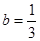时，分别求代数式①
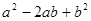②
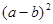的值；
（2）当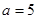
，
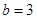时，分别求代数式①
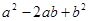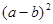②的值；
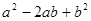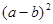（3）观察（1）（2）中代数式的值，与有何关系？
（4）利用你发现的规律，求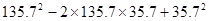
的值.
（本题5分）某服装店老板以60元的单价购进20件流行款的女服装，老板交代销售小姐以80元为标准价出售．针对不同的顾客，销售小姐对20件服装的售价不完全相同，她把超过80元的记为正数，其销售结果如下表所示：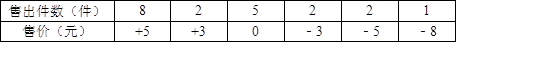
该服装店在售完这20件服装后，请你通过计算说明该服装店老板是赚钱还是亏本？如果赚钱，那么赚了多少钱？如果亏本，那么亏了多少钱？
（本题4分）已知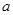
，
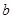互为倒数，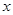
，
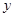互为相反数，
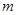是平方后为4的数．求代数式
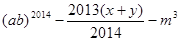的值.
（本题6分）已知
，
，
（1）求
的值；（结果用x、y表示）
（2）当
与
互为相反数时，求（1）中代数式的值.
化简求值（本题5分）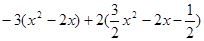
，其中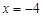
．[