雾霾天气严重影响市民的生活质量.在今年寒假期间,某校八年一班的综合实践小组同学对“雾霾天气的主要成因”随机调查了所在城市部分市民,并对调查结果进行了整理,绘制了如下不完整的统计图表,观察分析并回答下列问题.

(1)本次被调查的市民共有多少人?
(2)分别补全条形统计图和扇形统计图,并计算图2中区域B所对应的扇形圆心角的度数.
(3)若该市有100万人口,请估计持有A、B两组主要成因的市民有多少人?

如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=21cm,点P从点A开始沿AD边向D以1cm/s的速度移动,点Q从点C开始沿CB边向B以2cm/s的速度移动,如果P、Q分别从A、C同时出发,设移动的时间为t(s),求:
(1)t为何值时,四边形PQCD为平行四边形;
(2)t为何值时,四边形ABQP为矩形;
(3)t为何值时,梯形PQCD是等腰梯形。
某数学兴趣小组在本校九年级学生中以“你最喜欢的一项体育运动”为主题进行了抽样调查,并将调查结果绘制成如图图表:
| 项目 |
篮球 |
乒乓球 |
羽毛球 |
跳绳 |
其他 |
| 人数 |
a |
12 |
10 |
5 |
8 |

请根据图表中的信息完成下列各题:
(1)本次共调查学生名;
(2)a=,表格中五个数据的中位数是;
(3)在扇形图中,“跳绳”对应的扇形圆心角是°;
(4)如果该年级有450名学生,那么据此估计大约有人最喜欢“乒乓球”.
如图,在△ABC中,AB=AC,D,E分别是AB,AC的中点.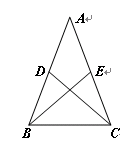
(1)试说明BE=CD;
(2)请用一句话叙述由第(1)小题得出的结论.
如图,正方形的边长为x,用代数式表示图中阴影部分的面积,并计算当 时,阴影部分的面积.(
时,阴影部分的面积.( 取3.14)
取3.14)
已知函数图象如图所示,根据图象可得:
(1)抛物线顶点坐标;
(2)对称轴为;
(3)当x=时,y有最大值是;
(4)当时,y随着x得增大而增大。
(5)当时,y>0.