如图,已知,在△ABC中,CA=CB,∠ACB=90°,E,F分别是CA,CB边的三等分点,将△ECF绕点C逆时针旋转α角(0°<α<90°),得到△MCN,连接AM,BN.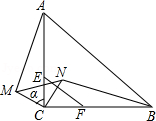
(1)求证:AM=BN;
(2)当MA∥CN时,试求旋转角α的余弦值.
已知:直角梯形ABCD中,DC⊥BC,AD∥BC,AD=AB=5,BC=8.动点P以1个单位/秒的速度从C开始,沿C—D—A方向运动,到达点A时停止.
(1)设△BCP的面积为y,运动的时间为t秒. 求y关于t的函数关系式,并写出t的范围;
(2)连接AP,当点P在CD上时,求在第几秒时,△ABP的面积与△BCP的面积相等?
(3)若在点P从点C出发的同时,另一动点M从A开始沿着A—D—C方向运动,运动速度为2个单位/秒. 求当P、M相遇时,△BCP的面积?
为弘扬体育精神,锻炼师生体魄,我校组织了今年春季运动会.在男子100米预赛中,高二年级某同学甲在发令枪响的同时立即起跑,起跑后甲与起点的距离与甲起跑后的时间大致满足正比例函数的关系.如果用y(米)表示与起点的距离,用x(秒)表示起跑后的时间,测得两个瞬间的x、y如下表:
| 起跑后的时间x(秒) |
3 |
9 |
| 与起跑点距离y(米) |
24 |
72 |
(1)求同学甲跑动过程中的函数关系式,并写出x的取值范围?
(2)如果同组另一位同学乙在发令枪响后与起点的距离与发令枪响后的时间大致满足下面的图像,请问:同学乙能否超越同学甲?若能,请通过计算求出在何时超越?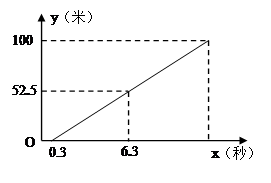
如图,平面直角坐标系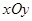 中,直线AB分别与
中,直线AB分别与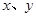 轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥
轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥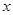 轴于点E,点C坐标是(-2,3),点D的坐标是(6,n).
轴于点E,点C坐标是(-2,3),点D的坐标是(6,n).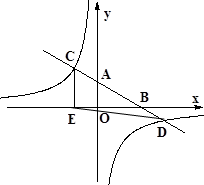
(1)求一次函数和反比例函数的表达式;
(2)求△DCE的面积.
已知变量y+1与(x-1)成反比例,且当x=2时,y=0.
(1)求y与x的函数关系式;(2)若 ,求此时的x值.
,求此时的x值.
若a、b满足a+2b=0且ab≠0,求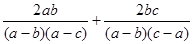 的值.
的值.