已知抛物线的顶点是 (
( ,
,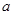 为常数),并经过点
为常数),并经过点 点
点 为一定点.
为一定点.
求含有常数
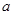 的抛物线的解析式;
的抛物线的解析式;设点P是抛物线上任意一点,过P作PH⊥
 轴,垂足是H,求证:PD=PH;
轴,垂足是H,求证:PD=PH;设过原点O的直线与抛物线在第一象限相交A、B两点,若DA=2DB,且
 ,求
,求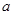 的值
的值
求不等式组 的最小整数解.
的最小整数解.
如图①,在□ABCD中,对角线AC⊥AB,BC=10,tan∠B=2.点E是BC边上的动点,过点E作EF⊥BC于点E,交折线AB-AD于点F,以EF为边在其右侧作正方形EFGH,使EH边落在射线BC上.点E从点B出发,以每秒1个单位的速度在BC边上运动,当点E与点C重合时,点E停止运动,设点E的运动时间为t( )秒.
)秒.
(1)□ABCD的面积为;当t=秒时,点F与点A重合;
(2)点E在运动过程中,连接正方形EFGH的对角线EG,得△EHG,设△EHG与△ABC的重叠部分面积为S,请直接写出S与t的函数关系式以及对应的自变量t的取值范围;
(3)作点B关于点A的对称点Bˊ,连接CBˊ交AD边于点M(如图②),当点F在AD边上时,EF与对角线AC交于点N,连接MN得△MNC.是否存在时间t,使△MNC为等腰三角形?若存在,请求出使△MNC为等腰三角形的时间t;若不存在,请说明理由.
如图,在平面直角坐标系中,△ABC的边AB在x轴上,∠ABC=90°,AB=BC,OA=1,OB=4,抛物
线 经过A、C两点.
经过A、C两点.
(1)求抛物线的解析式及其顶点坐标;
(2)如图①,点P是抛物线上位于x轴下方的一点,点Q与点P关于抛物线的对称轴对称,过点P、Q分别向x轴作垂线,垂足为点D、E,记矩形DPQE的周长为d,求d的最大值,并求出使d最大值时点P的坐标;
(3)如图②,点M是抛物线上位于直线AC下方的一点,过点M作MF⊥AC于点F,连接MC,作MN∥BC交直线AC于点N,若MN将△MFC的面积分成2:3两部分,请确定M点的坐标.
如图,△ABC中,∠ABC=45°,过点C作CD⊥AB于点D,过点B作BM⊥AC于点M,BM交CD于点E,且点E为CD的中点,连接MD,过点D作ND⊥MD于点D,DN交BM于点N.
(1)若BC=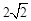 ,求△BDE的周长;
,求△BDE的周长;
(2)求证:NE-ME=CM.
重庆一中注重对学生的综合素质培养,每期都将开展丰富多彩的课外活动.3月中旬,在满园的樱花树下,初一、二年级举行了“让我们一起静听花开的声音”大型诗歌朗诵会,年级各班级积极参与.学校为鼓励同学们的积极性,对参与班级进行了奖励,分设一、二、三、四等级奖励,在给予精神奖励的同时也给与一定的物质奖励,为各个等级购买了一个相应的奖品.根据获奖情况,某初三同学绘制出如下两幅不完整的统计图,四个等级奖励的奖品价格用表格表示.
| 等级 |
价格(元/个) |
| 一等 |
100 |
| 二等 |
60 |
| 三等 |
40 |
| 四等 |
20 |
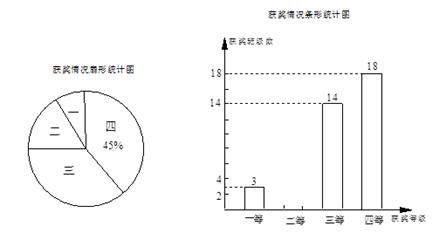
(1)两年级共有个班级参加此次活动,其中获得二等奖的班级有个,请补全条形统计图;
(2)在扇形统计图中,三等奖所在扇形的圆心角的度数是度,这些奖品的平均价格是元;
(3)在此次活动中,获得一等奖的班级中有两个班级来自初一年级,获得二等奖的班级中也只有两个班级来自初一年级.学校准备从获得一、二等奖的班级中各选出一个班级代表学校参加区级比赛,请你用画树状图或列表格的方法求出所选班级来自同一年级的概率.