(本小题满分16分)如图,在平面直角坐标系 中,椭圆
中,椭圆 的离心率为
的离心率为 ,直线
,直线 与
与 轴交于点
轴交于点 ,与椭圆
,与椭圆 交于
交于 、
、 两点.当直线
两点.当直线 垂直于
垂直于 轴且点
轴且点 为椭圆
为椭圆 的右焦点时, 弦
的右焦点时, 弦 的长为
的长为 .
.
(1)求椭圆 的方程;
的方程;
(2)若点 的坐标为
的坐标为 ,点
,点 在第一象限且横坐标为
在第一象限且横坐标为 ,连结点
,连结点 与原点
与原点 的直线交椭圆
的直线交椭圆 于另一点
于另一点 ,求
,求 的面积;
的面积;
(3)是否存在点 ,使得
,使得 为定值?若存在,请指出点
为定值?若存在,请指出点 的坐标,并求出该定值;若不存在,请说明理由.
的坐标,并求出该定值;若不存在,请说明理由.
已知某商品的进货单价为1元/件,商户甲往年以单价2元/件销售该商品时,年销量为1万件,今年拟下调销售单价以提高销量,增加收益.据测算,若今年的实际销售单价为x元/件(1≤x≤2),今年新增的年销量(单位:万件)与(2-x)2成正比,比例系数为4.
(1)写出今年商户甲的收益y(单位:万元)与今年的实际销售单价x间的函数关系式;
(2)商户甲今年采取降低单价,提高销量的营销策略是否能获得比往年更大的收益(即比往年收益更多)?说明理由.
在长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=a,E,F分别为AD,CD的中点.
(1)若AC1⊥D1F,求a的值;
(2)若a=2,求二面角E-FD1-D的余弦值.
在平面直角坐标系xOy中,曲线y=x2-2x-3与坐标轴的交点都在圆C上.
(1)求圆C的方程;
(2)若直线x+y+a=0与圆C交于A,B两点,且AB=2,求实数a的值.
已知m∈R,设p:复数z1=(m-1)+(m+3)i (i是虚数单位)在复平面内对应的点在第二象限,q:复数z2=1+(m-2)i的模不超过 .
.
(1)当p为真命题时,求m的取值范围;
(2)若命题“p且q”为假命题,“p或q”为真命题,求m的取值范围.
已知函数 ,
,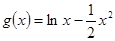 。
。
(1)求函数 的解析式;
的解析式;
(2)若对于任意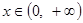 ,都有
,都有 成立,求实数
成立,求实数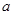 的取值范围;
的取值范围;
(3)设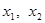 ,
, ,且
,且 ,求证:
,求证: 。
。