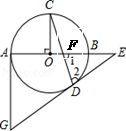
(本小题满分8分)如图,在⊙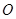 中,
中,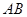 为直径,
为直径,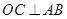 ,弦
,弦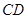 与
与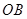 交于点
交于点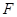 ,过点
,过点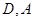 分别作⊙
分别作⊙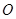 的切线交于点
的切线交于点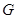 ,且GD与
,且GD与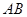 的延长线交于点
的延长线交于点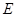 .
.
(1)求证: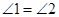 ;
;
(2)已知: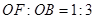 ,⊙
,⊙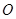 的半径为
的半径为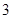 ,求
,求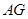 的长.
的长.
已知关于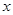 的一元二次方程
的一元二次方程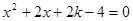 有两个不相等的实数根.
有两个不相等的实数根.
(1)求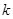 的取值范围;
的取值范围;
(2)若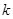 为正整数,且该方程的根都是整数,求
为正整数,且该方程的根都是整数,求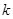 的值.
的值.
已知方程 的一个根是3,求m的值及方程的另一个根.
的一个根是3,求m的值及方程的另一个根.
先化简,再求值:( -1+
-1+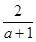 )÷(
)÷(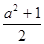 ),其中
),其中 =
= -1.
-1.
如图,四边形ABCD中,AD∥BC,AD=15,BC=25,AB=DC=10,动点P从点D出发,以每秒1个单位长的速度沿线段DA的方向向点A运动,动点Q从点C出发,以每秒2个单位长的速度沿射线CB的方向运动,点P、Q分别从点D、C同时出发,当点P运动到点A时,点Q随之停止运动.设运动的时间为t(秒).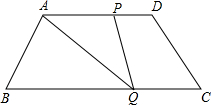
(1)当t=2时,求△APQ的面积;
(2)若四边形ABQP为平行四边形,求运动时间t;
(3)当t为何值时,以A、P、Q三点为顶点的三角形是等腰三角形?
商场某种新商品每件进价是120元,在试销期间发现,当每件商品售价为130元时,每天可销售70件,当每件商品售价高于130元时,每涨价1元,日销售量就减少1件.据此规律,请回答:
(1)当每件商品售价定为170元时,每天可销售多少件商品商场获得的日盈利是多少?
(2)在上述条件不变,商品销售正常的情况下,每件商品的销售价定为多少元时,商场日盈利可达到1600元?