【2015高考四川,文20】如图,椭圆E: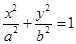 (a>b>0)的离心率是
(a>b>0)的离心率是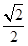 ,点P(0,1)在短轴CD上,且
,点P(0,1)在短轴CD上,且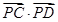 =-1
=-1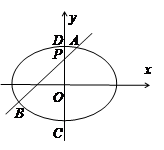
(Ⅰ)求椭圆E的方程;
(Ⅱ)设O为坐标原点,过点P的动直线与椭圆交于A、B两点.是否存在常数λ,使得 为定值?若存在,求λ的值;若不存在,请说明理由.
为定值?若存在,求λ的值;若不存在,请说明理由.
(本小题满分12分)已知函数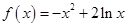 .
.
(Ⅰ)求函数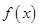 的最大值;
的最大值;
(Ⅱ)若函数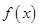 与
与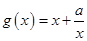 有相同极值点.
有相同极值点.
①求实数 的值;
的值;
②若对于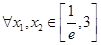 (
(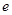 为自然对数的底数),不等式
为自然对数的底数),不等式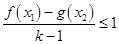 恒成立,求实数
恒成立,求实数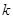 的取值范围.
的取值范围.
(本小题满分12分)已知椭圆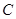 的中心在坐标原点,离心率
的中心在坐标原点,离心率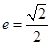 ,且其中一个焦点与抛物线
,且其中一个焦点与抛物线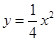 的焦点重合.
的焦点重合.
(Ⅰ)求椭圆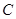 的方程;
的方程;
(Ⅱ)过点 的动直线
的动直线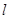 交椭圆
交椭圆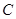 于
于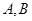 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点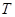 ,使得无论
,使得无论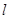 如何转动,以
如何转动,以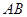 为直径的圆恒过点
为直径的圆恒过点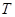 ?若存在,求出点
?若存在,求出点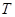 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
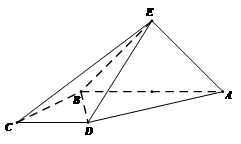
(本小题满分12分)如图,直角梯形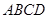 与等腰直角三角形
与等腰直角三角形 所在的平面互相垂直.
所在的平面互相垂直.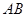 ∥
∥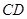 ,
,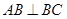 ,
, ,
,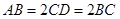 .
.
(Ⅰ)求证: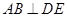 ;
;
(Ⅱ)求二面角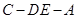 余弦值.
余弦值.
(本小题满分12分)某工厂生产甲、乙两种芯片,其质量按测试指标划分为:指标大于或等于82为合格品,小于82为次品.现随机抽取这两种芯片各100件进行检测,检测结果统计如下:
(Ⅰ)试分别估计芯片甲,芯片乙为合格品的概率;
(Ⅱ)生产一件芯片甲,若是合格品可盈利40元,若是次品则亏损5元;生产一件芯片乙,若是合格品可盈利50元,若是次品则亏损10元.在(Ⅰ)的前提下,记X为生产1件芯片甲和1件芯片乙所得的总利润,求随机变量X的概率分布列和数学期望值.
(本小题满分12分)已知 是公差为2的等差数列,且
是公差为2的等差数列,且 是
是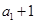 与
与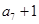 的等比中项.
的等比中项.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)令 ,求数列
,求数列 的前
的前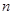 项和
项和 .
.