【2015高考天津,理16】(本小题满分13分)为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员3名,其中种子选手2名;乙协会的运动员5名,其中种子选手3名.从这8名运动员中随机选择4人参加比赛.
(Ⅰ)设A为事件“选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会”求事件A发生的概率;
(Ⅱ)设X为选出的4人中种子选手的人数,求随机变量X的分布列和数学期望.
(本小题满分14分)
已知函数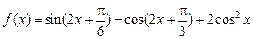 .
.
(1)求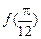 的值;
的值;
(2)求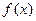 的最大值及相应
的最大值及相应 的值.
的值.
选修4—5:不等式选讲
已知函数
(1)解关于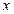 的不等式
的不等式 ;
;
(2)若函数 的图象恒在函数
的图象恒在函数 图象的上方,求
图象的上方,求 的取值范围。
的取值范围。
选修4—4:坐标系与参数方程
以直角坐标系的原点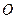 为极点,
为极点,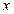 轴的正半轴为极轴,已知点
轴的正半轴为极轴,已知点 的直角坐标为
的直角坐标为 ,点
,点 的极坐标为
的极坐标为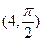 ,若直线
,若直线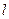 过点
过点 ,且倾斜角为
,且倾斜角为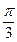 ,圆
,圆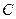 以
以 为圆心、
为圆心、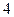 为半径。
为半径。
(1)求直线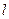 的参数方程和圆
的参数方程和圆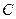 的极坐标方程;
的极坐标方程;
(2)试判定直线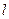 和圆
和圆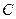 的位置关系。
的位置关系。
选做题.(本题满分10分.请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.作答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑.)
选修4—1:平面几何
如图,Δ
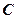 是内接于⊙O,
是内接于⊙O, ,直线
,直线 切⊙O于点
切⊙O于点 ,弦
,弦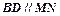 ,
,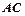 与
与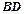 相交于点
相交于点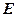 .
.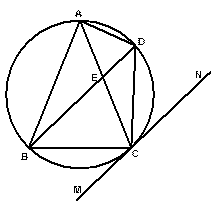
(1)求证:Δ ≌Δ
≌Δ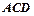 ;
;
(2)若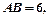
 ,求
,求 .
.
(本题满分12分)
如图的多面体是底面为平行四边形的直四棱柱ABCD—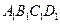 ,经平面AEFG所截后得到的图形.其中∠BAE=∠GAD=45°。AB=2AD=2.∠BAD=60。.
,经平面AEFG所截后得到的图形.其中∠BAE=∠GAD=45°。AB=2AD=2.∠BAD=60。.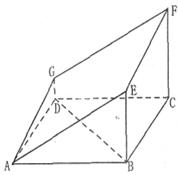
(I)求证:BD⊥平面ADG;
(Ⅱ)求平面AEFG与平面ABCD所成锐二面角的余弦值.