(本题满分12分)
如图的多面体是底面为平行四边形的直四棱柱ABCD—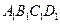
，经平面AEFG所截后得到的图形．其中∠BAE=∠GAD=45°。AB=2AD=2．∠BAD=60。．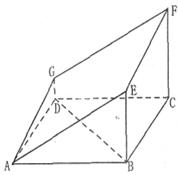
(I)求证：BD⊥平面ADG；
(Ⅱ)求平面AEFG与平面ABCD所成锐二面角的余弦值． 
已知极坐标系的极点与直角坐标系的原点重合，极轴与直角坐标系中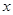
轴的正半轴重合，且两坐标系有相同的长度单位，圆C的参数方程为
（
为参数），点Q的极坐标为
。
（1）化圆C的参数方程为极坐标方程；
（2）直线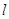
过点Q且与圆C交于M，N两点，求当弦MN的长度为最小时，直线的直角坐标方程。
如图，PA为⊙O的切线，A为切点，PBC是过点O的割线，PA=10，PB=5。
求：（1）⊙O的半径；
（2）s1n∠BAP的值。
已知函数
。
（1）若
，求
在
处的切线方程；
（2）若在R上是增函数，求实数
的取值范围。
已知椭圆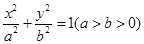
的一个顶点为B（0，4），离心率
，直线
交椭圆于M，N两点。
（1）若直线的方程为
，求弦MN的长；
（2）如果△BMN的重心恰好为椭圆的右焦点F，求直线方程的一般式。
如图，在四棱锥P－ABCD中，∠ABC=∠ACD=90°，∠BAC=∠CAD=60°，PA⊥平面ABCD,E为PD的中点，PA=2AB=2。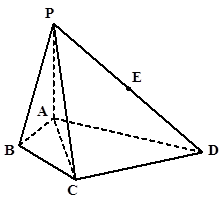
(1)求证：CE∥平面PAB;
(2)求四面体PACE的体积.