【2015高考广东,理17】某工厂36名工人的年龄数据如下表:
| 工人编号 |
年龄 |
工人编号 |
年龄 |
工人编号 |
年龄 |
工人编号 |
年龄 |
| 1 |
40 |
10 |
36 |
19 |
27 |
28 |
34 |
| 2 |
44 |
11 |
31 |
20 |
43 |
29 |
39 |
| 3 |
40 |
12 |
38 |
21 |
41 |
30 |
43 |
| 4 |
41 |
13 |
39 |
22 |
37 |
31 |
38 |
| 5 |
33 |
14 |
43 |
23 |
34 |
32 |
42 |
| 6 |
40 |
15 |
45 |
24 |
42 |
33 |
53 |
| 7 |
45 |
16 |
39 |
25 |
37 |
34 |
37 |
| 8 |
42 |
17 |
38 |
26 |
44 |
35 |
49 |
| 9 |
43 |
18 |
36 |
27 |
42 |
36 |
39 |
(1)用系统抽样法从36名工人中抽取容量为9的样本,且在第一分段里用随机抽样法抽到的年龄数据为44,列出样本的年龄数据;
(2)计算(1)中样本的平均值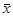 和方差
和方差 ;
;
(3)36名工人中年龄在 与
与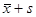 之间有多少人?所占的百分比是多少(精确到0.01%)?
之间有多少人?所占的百分比是多少(精确到0.01%)?
已知二次函数 .
.
(1)若 ,求满足
,求满足 的概率;
的概率;
(2)若 ,求满足
,求满足 的概率.
的概率.
某部门为了了解用电量 (单位:度)与气温x(单位:
(单位:度)与气温x(单位: )之间的关系,随机统计了某4天的用电量与当天气温,因某天统计的用电量数据丢失,用
)之间的关系,随机统计了某4天的用电量与当天气温,因某天统计的用电量数据丢失,用 表示,如下表:
表示,如下表:
气温( ) ) |
18 |
13 |
10 |
-1 |
| 用电量(度) |
24 |
t |
38 |
64 |
(1)由以上数据,求这4天气温的方差 .
(2)若用电量与气温之间具有较好的线性相关关系,回归直线方程为 ,且预测气温为
,且预测气温为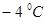 时,用电量为68度,求
时,用电量为68度,求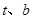 的值.
的值.
定义在R上的奇函数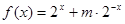 .
.
(1)求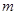 的值,并求当
的值,并求当 时,实数
时,实数 的取值范围;
的取值范围;
(2)当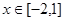 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
某班 位学生一次考试数学成绩的频率分布直方图如图,其中成绩分组区间是40,50), 50,60), 60,70),70,80),80,90),90,100.若成绩在区间70,90)的人数为34人.
位学生一次考试数学成绩的频率分布直方图如图,其中成绩分组区间是40,50), 50,60), 60,70),70,80),80,90),90,100.若成绩在区间70,90)的人数为34人.
(1)求图中 的值及
的值及 ;
;
(2)由频率分布直方图,求此次考试成绩平均数的估计值.
已知全集 , 集合
, 集合 ,
,  ,
, .
.
(1)求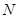 ∩
∩ ;
;
(2)若 ,求实数
,求实数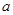 的取值范围.
的取值范围.