(本题9分)某中学开展“感恩父母”演讲比赛活动,八(1)、八(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示。
(1)根据下图,分别求出两班复赛的平均成绩和方差;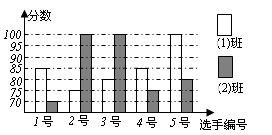
(2)根据(1)的计算结果,哪个班级的复赛成绩较好?为什么?
如图,已知四个点A、B、C、D,根据下列要求画图: 
(1)画线段AB;
(2)画∠CDB;
(3)找一点P,使P既在直线AD上,又在直线BC上.
计算及解方程:
(1)化简:
(2)解方程:
(3)先化简,再求值: ,其中 , .
如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
(1)将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周.如图2,经过t秒后,OM恰好平分∠BOC.①求t的值;②此时ON是否平分∠AOC?请说明理由;
(2)在(1)问的基础上,若三角板在转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周,如图3,那么经过多长时间OC平分∠MON?请说明理由;
(3)在(2)问的基础上,经过多长时间OC平分∠MOB?请画图并说明理由. 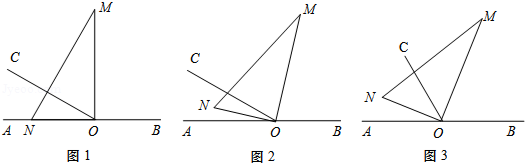
用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用).
A方法:剪6个侧面; B方法:剪4个侧面和5个底面.
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
“五•一”假期,某火车客运站旅客流量不断增大,旅客往往需要长时间排队等候检票.经调查发现,在车站开始检票时,有640人排队检票.检票开始后,仍有旅客继续前来排队检票进站.设旅客按固定的速度增加,检票口检票的速度也是固定的.检票时,每分钟候车室新增排队检票进站16人,每分钟每个检票口检票14人.已知检票的前a分钟只开放了两个检票口.某一天候车室排队等候检票的人数y(人)与检票时间x(分钟)的关系如图所示.
(1)求a的值.
(2)求检票到第20分钟时,候车室排队等候检票的旅客人数.
(3)若要在开始检票后15分钟内让所有排队的旅客都能检票进站,以便后来到站的旅客随到随检,问检票一开始至少需要同时开放几个检票口?