【2015高考新课标2,理19】
如图,长方体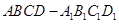 中,
中,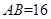 ,
, ,
,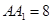 ,点
,点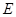 ,
,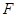 分别在
分别在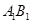 ,
,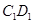 上,
上,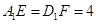 .过点
.过点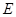 ,
,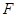 的平面
的平面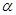 与此长方体的面相交,交线围成一个正方形.
与此长方体的面相交,交线围成一个正方形.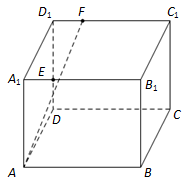
(Ⅰ)在图中画出这个正方形(不必说出画法和理由);
(Ⅱ)求直线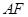 与平面
与平面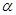 所成角的正弦值.
所成角的正弦值.
设x,y均为正数,且x>y,求证:2x+ ≥2y+3.
≥2y+3.
在平面直角坐标系xOy中,直线m的参数方程为 (t为参数);在以O为极点、射线Ox为极轴的极坐标系中,曲线C的极坐标方程为ρsin2θ=8cosθ.若直线m与曲线C交于A、B两点,求线段AB的长.
(t为参数);在以O为极点、射线Ox为极轴的极坐标系中,曲线C的极坐标方程为ρsin2θ=8cosθ.若直线m与曲线C交于A、B两点,求线段AB的长.
已知M= ,N=
,N= ,设曲线y=sinx在矩阵MN对应的变换作用下得到曲线F,求F的方程.
,设曲线y=sinx在矩阵MN对应的变换作用下得到曲线F,求F的方程.
如图,已知AB为圆O的直径,BC切圆O于点B,AC交圆O于点P,E为线段BC的中点.求证:OP⊥PE.
设函数f (x)的定义域为M,具有性质P:对任意x∈M,都有f (x)+f (x+2)≤2f (x+1).
(1)若M为实数集R,是否存在函数f (x)=ax (a>0且a≠1,x∈R) 具有性质P,并说明理由;
(2)若M为自然数集N,并满足对任意x∈M,都有f (x)∈N. 记d(x)=f (x+1)-f (x).
(ⅰ) 求证:对任意x∈M,都有d(x+1)≤d(x)且d(x)≥0;
(ⅱ) 求证:存在整数0≤c≤d(1)及无穷多个正整数n,满足d(n)=c.