(本小题满分12分)
已知椭圆 的右顶点为
的右顶点为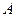 ,点
,点 在椭圆上,且它的横坐标为1,点
在椭圆上,且它的横坐标为1,点 ,且
,且 .
.
⑴求椭圆的方程;⑵若过点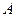 的直线
的直线 与椭圆交于另一点
与椭圆交于另一点 ,若线段
,若线段 的垂直平分线经过点
的垂直平分线经过点 ,求直线
,求直线 的方程.
的方程.
(本小题满分12分)
已知数列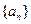 ,
,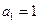 ,
,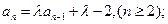
(Ⅰ)当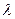 为何值时,数列
为何值时,数列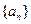 可以构成公差不为零的等差数列,并求其通项公式;
可以构成公差不为零的等差数列,并求其通项公式;
(Ⅱ)若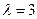 ,令
,令 ,求数列
,求数列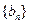 的前
的前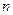 项和
项和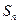 。
。
(本小题满分12分)
如图,有一块半径为1的半圆形钢板,计划剪成矩形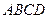 的形状,它的一边
的形状,它的一边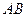 在圆
在圆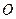 的直径上,另一边
的直径上,另一边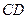 的端点在圆周上.求矩形
的端点在圆周上.求矩形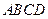 面积的最大值和周长的最大值.
面积的最大值和周长的最大值.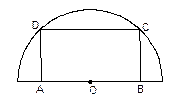
(本小题满分12分)
已知二次函数 的图象过点(0,-3),且
的图象过点(0,-3),且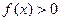 的解集
的解集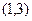 .
.
(Ⅰ)求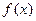 的解析式;
的解析式;
(Ⅱ)求函数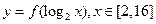 的最值.
的最值.
(本小题满分12分)
已知函数
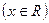 。
。
(Ⅰ)求函数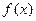 的最小正周期;
的最小正周期;
(Ⅱ)求函数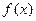 的单调递增区间,并写出对称轴方程.
的单调递增区间,并写出对称轴方程.
(本小题满分14分)
设函数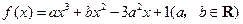 在
在 ,
,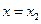 处取得极值,且
处取得极值,且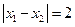 .
.
(Ⅰ)若 ,求
,求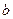 的值,并求
的值,并求 的单调区间;
的单调区间;
(Ⅱ)若 ,求
,求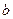 的取值范围.
的取值范围.