无穷数列  :
: ,
, ,……,
,……, ,……,满足
,……,满足 ,且
,且 ,对于数列
,对于数列 ,记
,记 ,其中
,其中 表示集合
表示集合 中最小的数.
中最小的数.
(1)若数列 :1,3,4,7,……,写出
:1,3,4,7,……,写出 ,
, ,……,
,……, ;
;
(2)若 ,求数列
,求数列 前
前 项的和;
项的和;
(3)已知 ,求
,求 的值.
的值.
(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知椭圆 (
( )的左、右焦点分别为
)的左、右焦点分别为 、
、 ,点
,点
 ,过点
,过点 且与
且与 垂直的直线交
垂直的直线交 轴负半轴于点
轴负半轴于点 ,且
,且 .
.
(1)求证:△ 是等边三角形;
是等边三角形;
(2)若过 、
、 、
、 三点的圆恰好与直线
三点的圆恰好与直线 :
: 相切,求椭圆
相切,求椭圆 的方程;
的方程;
(3)设过(2)中椭圆 的右焦点
的右焦点 且不与坐标轴垂直的直线
且不与坐标轴垂直的直线 与
与 交于
交于 、
、 两点,
两点, 是点
是点 关于
关于 轴的对称点.在
轴的对称点.在 轴上是否存在一个定点
轴上是否存在一个定点 ,使得
,使得 、
、 、
、 三点共线,若存在,求出点
三点共线,若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
本题共有2个小题,第1小题满分5分,第2小题满分9分.
某市环保部门对市中心每天的环境污染情况进行调查研究后,发现一天中环境综合污染指数 与时刻
与时刻 (时)的关系为
(时)的关系为 ,
, ,其中
,其中 是与气象有关的参数,且
是与气象有关的参数,且 .若用每天
.若用每天 的最大值为当天的综合污染指数,并记作
的最大值为当天的综合污染指数,并记作 .
.
(1)令 ,
, ,求
,求 的取值范围;
的取值范围;
(2)求 的表达式,并规定当
的表达式,并规定当 时为综合污染指数不超标,求当
时为综合污染指数不超标,求当 在什么范围内时,该市市中心的综合污染指数不超标.
在什么范围内时,该市市中心的综合污染指数不超标.
本题共有2个小题,第1小题满分6分,第2小题满分8分.
如图,四棱锥 的底面
的底面 为菱形,
为菱形, 平面
平面 ,
, ,
, ,
, 为
为 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求平面 与平面
与平面 所成的锐二面角大小的余弦值.
所成的锐二面角大小的余弦值.
本题共有2个小题,第1小题满分6分,第2小题满分6分.
在△ 中,已知
中,已知 ,外接圆半径
,外接圆半径 .
.
(1)求角 的大小;
的大小;
(2)若角 ,求△
,求△ 面积的大小.
面积的大小.
本题共有3个小题,第(1)小题满分4分,第(2)小题满分7分,第(3)小题满分7分.
各项均为正数的数列 的前
的前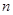 项和为
项和为 ,且对任意正整数
,且对任意正整数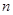 ,都有
,都有 .
.
(1)求数列 的通项公式;
的通项公式;
(2)如果等比数列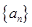 共有
共有 项,其首项与公比均为
项,其首项与公比均为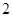 ,在数列
,在数列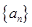 的每相邻两项
的每相邻两项 与
与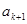 之间插入
之间插入 个
个 后,得到一个新的数列
后,得到一个新的数列 .求数列
.求数列 中所有项的和;
中所有项的和;
(3)如果存在 ,使不等式
,使不等式 成立,求实数
成立,求实数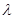 的范围.
的范围.