本题共有3个小题,第(1)小题满分4分,第(2)小题满分7分,第(3)小题满分7分.
各项均为正数的数列 的前
的前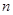 项和为
项和为 ,且对任意正整数
,且对任意正整数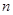 ,都有
,都有 .
.
(1)求数列 的通项公式;
的通项公式;
(2)如果等比数列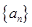 共有
共有 项,其首项与公比均为
项,其首项与公比均为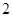 ,在数列
,在数列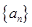 的每相邻两项
的每相邻两项 与
与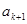 之间插入
之间插入 个
个 后,得到一个新的数列
后,得到一个新的数列 .求数列
.求数列 中所有项的和;
中所有项的和;
(3)如果存在 ,使不等式
,使不等式 成立,求实数
成立,求实数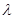 的范围.
的范围.
已知四棱锥P-ABCD的底面ABCD是边长为1的正方形,PD⊥底面ABCD,PD="AD." 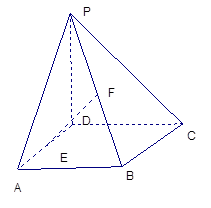
(Ⅰ)求证:BC∥平面PAD;
(Ⅱ)若E、F分别为PB,AD的中点,求证:EF⊥BC;
(Ⅲ)求二面角C-PA-D的余弦值.
已知A,B,C,D四个城市,它们各自有一个著名的旅游点,依次记为A,b,C,D,把A,B,C,D和A,b,C,D分别写成左、右两列.现在一名旅游爱好者随机用4条线把城市与旅游点全部连接起来, 构成“一一对应”.规定某城市与自身的旅游点相连称为“连对”,否则称为“连错”,连对一条得2分,连错一条得0分.
(Ⅰ)求该旅游爱好者得2分的概率.
(Ⅱ)求所得分数 的分布列和数学期望.
的分布列和数学期望.
在⊿ABC中,角A,B,C的对边分别为A,b,C,且满足(2A-C)CosB=bCosC.
(Ⅰ)求角B的大小;
(Ⅱ)已知函数f(A,C)=Cos2A+sin2C,求f(A,C)的最大值。
已知函数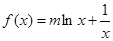 ,(其中m为常数).
,(其中m为常数).
(1) 试讨论 在区间
在区间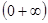 上的单调性;
上的单调性;
(2) 令函数 .当
.当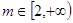 时,曲线
时,曲线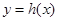 上总存在相异两点
上总存在相异两点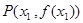 、
、 ,使得过
,使得过 、
、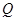 点处的切线互相平行,求
点处的切线互相平行,求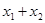 的取值范围.
的取值范围.
如图,椭圆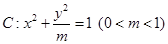 的左顶点为
的左顶点为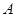 ,
, 是椭圆
是椭圆 上异于点
上异于点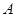 的任意一点,点
的任意一点,点 与点
与点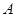 关于点
关于点 对称.
对称.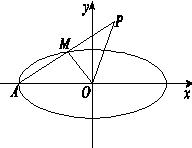
(1)若点 的坐标为
的坐标为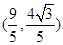 ,求
,求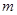 的值;
的值;
(2)若椭圆 上存在点
上存在点 ,使得
,使得 ,求
,求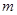 的取值范围.
的取值范围.