在四棱锥V-ABCD中，底面ABCD是正方形，侧面VAD是正三角形，平面VAD⊥底面ABCD．
（Ⅰ）证明AB⊥平面VAD；
（Ⅱ）求面VAD与面VDB所成二面角的大小。
已知椭圆C的中心在坐标原点，焦点在x轴上，椭圆C上的点到焦点距离的最大值为3，最小值为1.
（1）求椭圆C的标准方程
（2）若直线L：y=kx+m与椭圆C相交于A,B两点（A,B不是左右顶点），且以AB为直径的圆过椭圆C的右顶点D.求证：直线L过定点，并求处该定点的坐标。
已知函数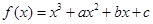
在
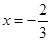与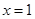
时都取得极值
（1）求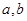
的值；
（2）若对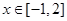
，不等式
恒成立，求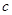
的取值范围.
在圆
上任取一点P，过点P作x轴的垂线段PD,D为垂足.当点P在圆上运动时，线段PD的中点M的轨迹方程，指出轨迹是什么？并求出该轨迹的焦点和离心率.
设函数
．
（1）求函数
的单调区间.
（2）若方程
有且仅有三个实根，求实数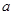
的取值范围.
已知：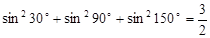
; 
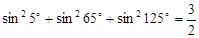
通过观察上述两等式的规律，请你写出一般性的命题，并给出的证明.