【2015高考安徽,理19】如图所示,在多面体 ,四边形
,四边形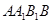 ,
, 均为正方形,
均为正方形, 为
为 的中点,过
的中点,过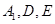 的平面交
的平面交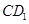 于F.
于F.
(Ⅰ)证明: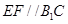 ;
;
(Ⅱ)求二面角 余弦值.
余弦值.
甲有一个箱子,里面放有x个红球,y个白球(x,y≥0,且x+y=4);乙有一个箱子,里面放有2个红球,1个白球,1个黄球.现在甲从箱子里任取2个球,乙从箱子里任取1个球.若取出的3个球颜色全不相同,则甲获胜.
(1)试问甲如何安排箱子里两种颜色球的个数,才能使自己获胜的概率最大?
(2)在(1)的条件下,求取出的3个球中红球个数的期望.
调查在2~3级风时的海上航行中男女乘客的晕船情况,共调查了71人,其中女性34人,男性37人。女性中有10人晕船,另外24人不晕船;男性中有12人晕船,另外25人不晕船。
判断晕船是否与性别有关系。
求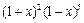 的展开式中
的展开式中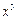 的系数.
的系数.
为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
| 组 别 |
频数 |
频率 |
| 145. 5~149.5 |
1 |
0.02 |
| 149.5~153.5 |
4 |
0.08 |
| 153.5~157.5 |
20 |
0.40 |
| 157.5~161.5 |
15 |
0.30 |
| 161.5~165.5 |
8 |
0.16 |
| 165.5~169.5 |
m |
n |
| 合 计 |
M |
N |
(1)求出表中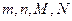 所表示的数分别是多少?
所表示的数分别是多少?
(2)画出频率分布直方图.
(3)全体女生中身高在哪组范围内的人数最多?
已知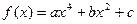 的图象经过点
的图象经过点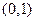 ,且在
,且在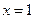 处的切线方程是
处的切线方程是
求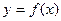 的解析式;
的解析式;