(本小题满分13分)某高校在上学期依次举行了“法律、环保、交通”三次知识竞赛活动,要求每位同学至少参加一次活动.该高校2014级某班50名学生在上学期参加该项活动的次数统计如图所示
(1)从该班中任意选两名学生,求他们参加活动次数不相等的概率.
(2)从该班中任意选两名学生,用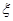 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量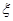 的分布列及数学期望
的分布列及数学期望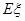 .
.
(3)从该班中任意选两名学生,用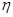 表示这两人参加活动次数之和,记“函数
表示这两人参加活动次数之和,记“函数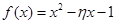 在区间(3,5)上有且只有一个零点”为事件A,求事件A发生的概率.
在区间(3,5)上有且只有一个零点”为事件A,求事件A发生的概率.
已知圆 :
: ,点
,点 ,
, ,点
,点 在圆
在圆 上运动,
上运动, 的垂直平分线交
的垂直平分线交 于点
于点 .
.
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)设 分别是曲线
分别是曲线 上的两个不同点,且点
上的两个不同点,且点 在第一象限,点
在第一象限,点 在第三象限,若
在第三象限,若 ,
, 为坐标原点,求直线
为坐标原点,求直线 的斜率
的斜率 ;
;
(3)过点 且斜率为
且斜率为 的动直线
的动直线 交曲线
交曲线 于
于 两点,在
两点,在 轴上是否存在定点
轴上是否存在定点 ,使以
,使以 为直径的圆恒过这个点?若存在,求出
为直径的圆恒过这个点?若存在,求出 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
已知椭圆 的方程为
的方程为 ,双曲线
,双曲线 的两条渐近线为
的两条渐近线为 ,
, ,过椭圆
,过椭圆 的右焦点
的右焦点 作直线
作直线 ,使
,使 ⊥
⊥ ,又l与
,又l与 交于
交于 点,设
点,设 与椭圆
与椭圆 的两个交点由上至下依次为
的两个交点由上至下依次为 .
.
(1)当 与
与 夹角为60°,双曲线的焦距为4时,求椭圆
夹角为60°,双曲线的焦距为4时,求椭圆 的方程及离心率;
的方程及离心率;
(2)求 的最大值.
的最大值.
已知抛物线的顶点在原点,焦点在 轴正半轴上,抛物线上一点的横坐标为2,且该点到焦点的距离为2.
轴正半轴上,抛物线上一点的横坐标为2,且该点到焦点的距离为2.
(1)求抛物线的标准方程;
(2)与圆 相切的直线
相切的直线 交抛物线于不同的两点
交抛物线于不同的两点 ,若抛物线上一点
,若抛物线上一点 满足
满足 ,求
,求 的取值范围。
的取值范围。
已知“ ,使等式
,使等式 成立”是真命题.
成立”是真命题.
(1)求实数 的取值集合
的取值集合 ;
;
(2)设不等式 解集为
解集为 ,若
,若 是
是 的必要条件,求实数
的必要条件,求实数 的取值范围.
的取值范围.
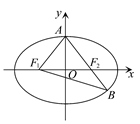
如图,已知椭圆 ,
,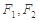 分别为椭圆的左、右焦点,
分别为椭圆的左、右焦点,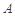 为椭圆的上顶点,直线
为椭圆的上顶点,直线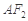 交椭圆于另一点
交椭圆于另一点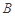 .
.
(1)若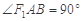 ,求椭圆的离心率;
,求椭圆的离心率;
(2)若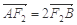 ,
, ,求椭圆的方程.
,求椭圆的方程.