(本小题满分13分)某校高一年级开设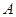 ,
,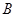 ,
,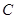 ,
,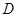 ,
,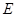 五门选修课,每位同学须彼此独立地选三门课程,其中甲同学必选
五门选修课,每位同学须彼此独立地选三门课程,其中甲同学必选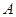 课程,不选
课程,不选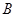 课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
(Ⅰ)求甲同学选中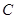 课程且乙同学未选中
课程且乙同学未选中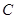 课程的概率;
课程的概率;
(Ⅱ)用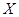 表示甲、乙、丙选中
表示甲、乙、丙选中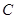 课程的人数之和,求
课程的人数之和,求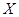 的分布列和数学期望.
的分布列和数学期望.
.
如图 1,平面四边形ABCD关于直线AC对称,
1,平面四边形ABCD关于直线AC对称,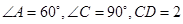 ,把△ABD沿BD折起(如图2),
,把△ABD沿BD折起(如图2), 使二面角A―BD―C的余弦值等于
使二面角A―BD―C的余弦值等于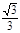 。对于图2,完成以下各小题:
。对于图2,完成以下各小题: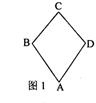
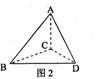
(1)求A,C两点间的距离;
(2)证明:AC 平面BCD;
平面BCD;
(3)求直线AC与平面ABD所成角的正弦值。
已知函数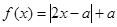 。
。
(1)若不等式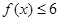 的解集为
的解集为
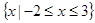 ,求实数
,求实数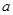 的值;
的值;
(2)在(1)的条件下,若存在实数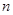 使
使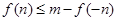 成立,求实数m的取值范围。
成立,求实数m的取值范围。
用总长14.8m的钢条制成一个长方体容器的框架,如果所制做容器的底面的一边比另一边长0.5m,那么高为多少时容器的容积最大?并求出它的最大容积。
已知数列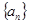 是递增数列,且满足
是递增数列,且满足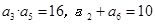 。
。
(1)若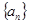 是等差数列,求数列
是等差数列,求数列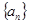 的通项公式;
的通项公式;
(2)对于(1)中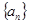 ,令
,令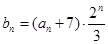 ,求数列
,求数列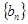 的前
的前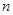 项和
项和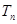 。
。
已知两点A 。
。
(1)求 的对称轴和对称中心;
的对称轴和对称中心;
(2)求 的单调递增区间。
的单调递增区间。