观察下列各式:
1=12,
2+3+4=32,
3+4+5+6+7=52,
4+5+6+7+8+9+10=72,
…,可以得出的一般结论是( )
| A.n+(n+1)+(n+2)+…+(3n-2)=n2 |
| B.n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2 |
| C.n+(n+1)+(n+2)+…+(3n-1)=n2 |
| D.n+ (n+1)+(n+2)+…+(3n-1)=(2n-1)2 |
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,φ∈R),则“f(x)是奇函数”是“φ= ”的( ).
”的( ).
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
将函数y=sin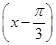 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图象向左平移 个单位,则所得函数图象对应的解析式为( ).
个单位,则所得函数图象对应的解析式为( ).
A.y=sin |
B.y=sin |
C.y=sin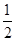 x x |
D.y=sin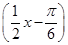 |
设函数f(x)满足x2f′(x)+2xf(x)=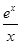 ,f(2)=
,f(2)=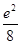 ,则x>0时,f(x)( ).
,则x>0时,f(x)( ).
| A.有极大值,无极小值 |
| B.有极小值,无极大值 |
| C.既有极大值又有极小值 |
| D.既无极大值也无极小值 |
已知f(x)是定义在(0,+∞) 上的非负可导函数,且满足xf′(x)+f(x)≤0,对任意的0<a<b,则必有( ).
| A.af(b)≤bf(a) | B.bf(a)≤af(b) |
| C.af(a)≤f(b) | D.bf(b)≤f(a) |
函数f(x)的定义域是R,f(0)=2,对任意x∈R,f(x)+f′(x)>1,则不等式ex·f(x)>ex+1的解集为( ).
A. |
B. |
C. |
D. |