在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF=∠CEF=45°．
（1）将△ADF绕着点A顺时针旋转90°，得到△ABG（如图①），求证：△AEG≌△AEF；
（2）若直线EF与AB，AD的延长线分别交于点M，N（如图②），求证：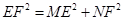
；
（3）将正方形改为长与宽不相等的矩形，若其余条件不变（如图③），请你直接写出线段EF，BE，DF之间的数量关系．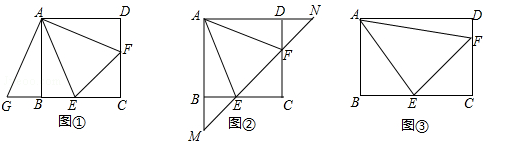
如图，有一面积为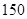
米2的长方形鸡场，鸡场的一边靠墙（墙长
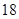米），另三边用竹篱笆围成，如果竹篱笆的长为
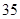米，求鸡场的长与宽各为多少米？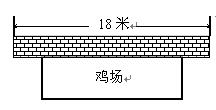
如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连结AC，过点D作DE⊥AC，垂足为E．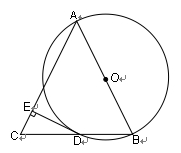
（1）求证：AB=AC；(2)求证DE为⊙O的切线．
如图，一个圆锥的高为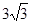
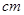,侧面展开图是半圆，求：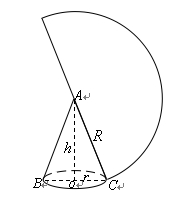
（1）圆锥的底面半径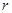
与母线
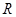之比；
（2）圆锥的全面积．
已知关于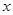
的一元二次方程
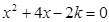有两个实数根，求
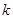的取值范围及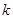的负整数值．
如图，在破残的圆形残片上，弦AB的垂直平分线交弧AB于点C，交弦AB于点D，已知AB=8cm，CD=2cm．
（1）求作此残片所在的圆（不写作法，保留作图痕迹）；
（2）求出（1）中所作圆的半径．