如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2;
(3)求出(2)中C点旋转到C2点所经过的路径长(记过保留根号和π).
解方程
(1)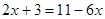
(2)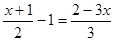
计算
(1) 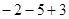
(2)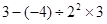
(3)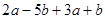
(4)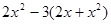
下列各图是由若干花盆组成的形如正方形的图案,每条边(包括两个顶点)有n(n>1)个花盆,每个图案花盆总数是S.
(1)按要求填表: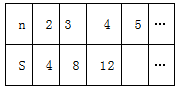
| n |
2 |
3 |
4 |
5 |
6 |
… |
| S |
4 |
8 |
12 |
… |
(2)写出当n=10时,S=.
(3)写出花盆总数S与n的关系式:S=.
(4)用42个花盆能摆出类似的图案吗?为什么?
已知:a与b互为相反数,c与d互为倒数,m的绝对值是2,求代数式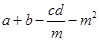 的值.
的值.
一只小虫从某点P出发,在一条直线上来回爬行,若把向右爬行的路程记为正数,向左爬行的路程记为负数,则爬行各段路程(单位:厘米)依次为:+5,-3,+10,-8,-6,+12,-10.
(1)通过计算说明小虫是否回到起点P.
(2)如果小虫爬行的速度为0.5厘米/秒,那么小虫共爬行了多长时间.