我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线, AF⊥BE , 垂足为P.像△ABC这样的三角形均为“中垂三角形”.设
 ,
, ,
, .
.
特例探索
(1)如图1,当∠ =45°,
=45°, 时,
时, = ,
= , ;
;
如图2,当∠ =30°,
=30°, 时,
时,  = ,
= , ;
;

归纳证明
(2)请你观察(1)中的计算结果,猜想 三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;
三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;
拓展应用
(3)如图4,在□ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG, AD=  ,AB=3.求AF的长.
,AB=3.求AF的长.

已知函数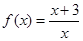 :
:
(1)写出此函数的定义域和值域;
(2)证明函数在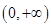 为单调递减函数;
为单调递减函数;
(3)试判断并证明函数 的奇偶性.
的奇偶性.
设集合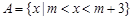 ,
, ,分别求满足下列条件的实数
,分别求满足下列条件的实数 的取值或取值范围:
的取值或取值范围:
(1)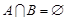 ;
;
(2)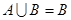 .
.
(1)求值: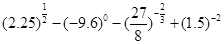 ;
;
(2)解不等式: .
.
(本小题满分14分)如图,椭圆 :
: 的左焦点为
的左焦点为 ,右焦点为
,右焦点为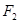 ,离心率
,离心率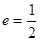 .过
.过 的直线交椭圆于
的直线交椭圆于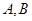 两点,且△
两点,且△ 的周长为
的周长为 .
.
(Ⅰ)求椭圆 的方程.
的方程.
(Ⅱ)设动直线 :
: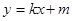 与椭圆
与椭圆 有且只有一个公共点
有且只有一个公共点 ,且与直线
,且与直线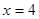 相交于点
相交于点 .试探究:在坐标平面内是否存在定点
.试探究:在坐标平面内是否存在定点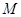 ,使得以
,使得以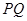 为直径的圆恒过点
为直径的圆恒过点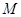 ?若存在,求出点
?若存在,求出点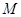 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(本小题13分)如图,棱锥 的底面
的底面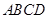 是矩形,
是矩形,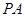 ⊥平面
⊥平面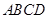 ,
,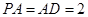 ,
,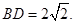

(1)求证: ⊥平面
⊥平面 ;
;
(2)求二面角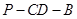 的大小;
的大小;
(3)求点 到平面
到平面 的距离.
的距离.