给出如下规定:两个图形G1和G2,点P为G1上任一点,点Q为G2上任一点,如果线段PQ的长度存在最小值,就称该最小值为两个图形G1和G2之间的距离.在平面直角坐标系xOy中,O为坐标原点.
(1)点A的坐标为 ,则点
,则点 和射线OA之间的距离为________,点
和射线OA之间的距离为________,点 和射线OA之间的距离为________;
和射线OA之间的距离为________;
(2)如果直线 和双曲线
和双曲线 之间的距离为
之间的距离为 ,那么k= ;(可在图1中进行研究)
,那么k= ;(可在图1中进行研究)
(3)点E的坐标为(1, ),将射线OE绕原点O逆时针旋转60°,得到射线OF,在坐标平面内所有和射线OE,OF之间的距离相等的点所组成的图形记为图形M.
),将射线OE绕原点O逆时针旋转60°,得到射线OF,在坐标平面内所有和射线OE,OF之间的距离相等的点所组成的图形记为图形M.
①请在图2中画出图形M,并描述图形M的组成部分;(若涉及平面中某个区域时可以用阴影表示)
②将射线OE,OF组成的图形记为图形W,抛物线 与图形M的公共部分记为图形N,请直接写出图形W和图形N之间的距离.
与图形M的公共部分记为图形N,请直接写出图形W和图形N之间的距离.

(本小题15分)
已知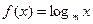 (m为常数,m>0且
(m为常数,m>0且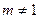 ),设
),设 是首项为4,公差为2的等差数列.
是首项为4,公差为2的等差数列.
(1)求证:数列{an}是等比数列;
(2)若bn=an·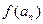 ,且数列{bn}的前n项和Sn,当
,且数列{bn}的前n项和Sn,当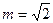 时,求
时,求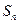 ;
;
(3)若cn=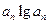 ,问是否存在m,使得{cn}中每一项恒小于它后面的项?若存在,
,问是否存在m,使得{cn}中每一项恒小于它后面的项?若存在,
求出m的范围;若不存在,说明理由.
(本小题10分)
某种汽车,购车费用是10万元,每年使用的保险费、养路费、汽油费约为0.9万元,年维修费第一年是0.2万元,以后逐年递增0.2万元,问这种汽车使用多少年时,它的年平均费用最少?最少是多少?
(本题10分)某家公司每月生产两种布料A和B,所有原料是两种不同颜色的羊毛,下表给出了生产每匹每种布料所需的羊毛量,以及可供使用的每种颜色的羊毛的总量。
| 羊毛颜色 |
每匹需要( kg) |
供应量(kg) |
|
| 布料A |
布料B |
||
| 红 |
4 |
4 |
1400 |
| 绿 |
6 |
3 |
1800 |
已知生产每匹布料A、B的利润分别为120元、80元。那么如何安排生产才能够产生最大的利润?最大的利润是多少?
(本小题10分)
已知△ABC的内角A、B、C所对的边分别为a,b,c,且a=2, cosB= .
.
(1)若b=4,求sinA的值;
(2) 若△ABC的面积S△ABC=4,求b,c的值.
(本题10分)
已知等差数列 满足
满足 ,
, 为
为 的前
的前 项和.
项和.
(1)求通项 及当
及当 为何值时,
为何值时, 有最大值,并求其最大值。
有最大值,并求其最大值。
(2)设 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列 的通项公式及其前
的通项公式及其前 项和
项和 .
.