如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒,当t为何值时,以P、Q、C为顶点的三角形与△ADE相似?
(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
一个三棱柱的底面是边长为3的正三角形,侧棱垂直于
底面,它的三视图如图所示, .
.
(1)请画出它的直观图;(2)求这个三棱柱的表面积和体积.
定义:若函数 在某一区间D上任取两个实数
在某一区间D上任取两个实数 、
、 ,且
,且 ,都有
,都有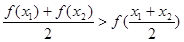 ,则称函数
,则称函数 在区间D上具有性质L。
在区间D上具有性质L。
(1)写出一个在其定义域上具有性质L的对数函数(不要求证明)。
(2)对于函数 ,判断其在区间
,判断其在区间 上是否具有性质L?并用所给定义证明你的结论。
上是否具有性质L?并用所给定义证明你的结论。
(3)若函数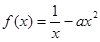 在区间(0,1)上具有性质L,求实数
在区间(0,1)上具有性质L,求实数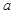 的取值范围。
的取值范围。
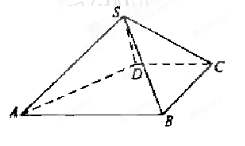
如图,四棱锥 中,
中, ,
,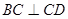 ,侧面
,侧面 为等边三角形,
为等边三角形,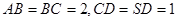 .
.
(Ⅰ)证明: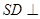 平面
平面 ;
;
(Ⅱ)求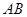 与平面
与平面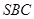 所成角的正弦值.
所成角的正弦值.
已知函数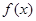 =
=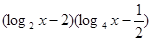 ,2≤
,2≤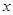 ≤4
≤4
(1)求该函数的值域;
(2)若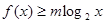 对于
对于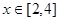 恒成立,求
恒成立,求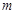 的取值范围.
的取值范围.
在长方体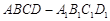 中,
中,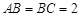 ,过
,过 、
、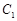 、
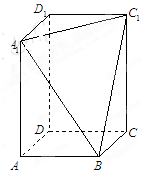
、 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体 ,且这个几何体的体积为
,且这个几何体的体积为 .
.
(1)求棱 的长;
的长;
(2)若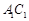 的中点为
的中点为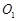 ,求异面直线
,求异面直线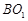 与
与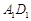 所成角的余弦值.
所成角的余弦值.