在甲、乙两个不透明的布袋，甲袋中装有3个完全相同的小球，分别标有数字0，1，2；乙袋中装有3个完全相同的小球，分别标有数字﹣1，﹣2，0；现从甲袋中随机抽取一个小球，记录标有的数字为x，再从乙袋中随机抽取一个小球，记录标有的数字为y，确定点M坐标为（x，y）．
（1）用树状图或列表法列举点M所有可能的坐标；
（2）求点M（x，y）在函数
的图象上的概率；
（3）在平面直角坐标系xOy中，⊙O的半径是2，求过点M（x，y）能作⊙O的切线的概率．
【挑战自我】
如图，已知PD⊥平面ABCD，AD⊥DC，AD∥BC，PD∶DC∶BC＝1∶1∶
.
（1）求二面角D－PB－C的正切值；
（2）当AD∶BC的值是多少时，能使平面PAB⊥平面PBC？证明你的结论.
已知椭圆方程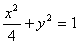
，过B（－1，0）的直线l交随圆于C、D两点，交直线x＝－4于E点，B、E分
的比分λ1、λ2．求证：λ1＋λ2＝0
在长方体ABCD—A1B1C1D1，中，AD=AA1=1，AB=2，点E在棱AB上移动.
（1）证明：D1E⊥A1D；
（2）当E为AB的中点时，求点E到面ACD1的距离；
（3）AE等于何值时，二面角D1—EC—D的大小为
.
如图，已知平行六面体ABCD—A1B1C1D1的底面是菱形且∠C1CB=∠C1CD=∠BCD=60°,
(1)证明
C1C⊥BD；
(2)假定CD=2，CC1=
，记面C1BD为α,面CBD为β,求二面角α—BD—β的平面角的余弦值；
(3)当
的值为多少时，可使A1C⊥面C1BD？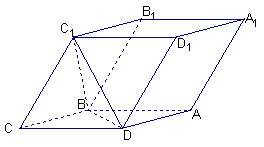
已知抛物线y=x2－1上一定点B(－1，0)和两个动点P、Q，当P在抛物线上运动时，BP⊥PQ，则Q点的横坐标的取值范围是_________