（本小题满分10分）已知函数
．
（1）求函数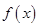
的定义域并判断函数的奇偶性；
（2）设
，若记
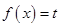，求函数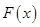
的最大值的表达式
．
(本小题满分12分)
已知命题p：
，
恒成立．命题q：
使得
．若“
且
”为真，求实数
的取值范围．
（本题14分）已知圆
和点
（1）若过点
有且只有一条直线与圆
相切，求实数
的值，并求出切线方程；
（2）若
，过点作圆的两条弦
，且互相垂直，求
的最大值。
（本小题满分13分）已知圆C的圆心在直线y=x+1上，且过点
（1，3），与直线x+2y-7=0相切.
（1）求圆C的方程；
（2）设直线
：
与圆C相交于A、B两点，求实数
的取值范围；
（3）在（Ⅱ）的条件下，是否存在实数，使得弦
的垂直平分线过点
，若存在，求出实数的值；若不存在，请说明理由．
如图5，已知直角梯形
所在的平面垂直于平面
，
，
，
．
（1）在直线
上是否存在一点
，使得
平面
？请证明你的结论；
（2）求平面
与平面所成的锐二面角
的余弦值。
(本题满分12分) 已知平面区域
恰好被面积最小的圆C：
及其内部覆盖．
（1）求圆C的方程；
（2）斜率为1的直线
与圆C交于不同两点A、B，且
，求直线的方程．