如图5,已知直角梯形 所在的平面垂直于平面
所在的平面垂直于平面 ,
, ,
, ,
,
 .
.
(1)在直线 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ?请证明你的结论;
?请证明你的结论;
(2)求平面 与平面
与平面 所成的锐二面角
所成的锐二面角 的余弦值。
的余弦值。
(13分) 已知函数 ,
,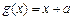 (a > 0)(1)求a的值,使点M(
(a > 0)(1)求a的值,使点M( ,
,  )到直线
)到直线 的最短距离为
的最短距离为 ;(2)若不等式
;(2)若不等式 在
在 [1,4]恒成立,求a的取值范围.
[1,4]恒成立,求a的取值范围.
(12分) 已知 ,
,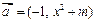 ,
, ,
,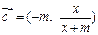 .
.
(1)当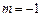 时,求使不等式
时,求使不等式 成立的x的取值范围;
成立的x的取值范围;
(2)当m﹥0时,求使不等式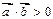 成立的x的取值范围.
成立的x的取值范围.
(12分) 已知向量 与
与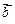 的夹角为30°,且|
的夹角为30°,且| |=
|= ,|
,|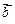 |=1,(1)求|
|=1,(1)求| -2
-2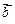 |的值;(2)设向量
|的值;(2)设向量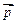 =
= +2
+2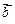 ,
, =
= -2
-2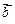 ,求向量
,求向量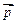 在
在 方向上的投影.
方向上的投影.
(12分)在△ABC中,|AB|=|AC|,∠A=120°,A(0,2),BC所在直线方程为x-y-1=0,求边AB、AC所在直线方程.
直角三角形 的顶点坐标
的顶点坐标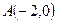 ,直角顶点
,直角顶点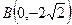 ,顶点
,顶点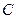 在
在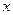 轴的正半轴上,点
轴的正半轴上,点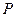 为线段
为线段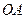 的中点
的中点
(1)求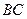 边所在直线方程。(2)M为直角三角形
边所在直线方程。(2)M为直角三角形 外接圆的圆心,求圆M的方程。
外接圆的圆心,求圆M的方程。
(3)若动圆N过点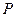 且与圆M内切,求动圆的圆心
且与圆M内切,求动圆的圆心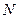 的轨迹方程。
的轨迹方程。