（本小题满分14分）经市场调查，某超市的一种小商品在过去的近20天内的销售量（件）与价格（元）均为时间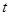
（天）的函数，且销售量近似满足
（件），价格近似满足
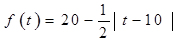（元）．
（1）试写出该种商品的日销售额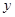
与时间（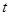
）的函数关系表达式；
（2）求该种商品的日销售额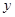的最大值与最小值
观察下列三角形数表
记第
行的第m个数为
．
（Ⅰ）分别写出
，
，
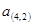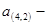
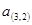值的大小；
（Ⅱ）归纳出
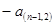的关系式，并求出关于n的函数表达式．
在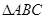
中，
分别是角A、B、C的对边，且满足：
．
（I）求C；
（II）当
时，求函数
的值域．
已知
，点B是
轴上的动点，过B作AB的垂线
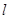交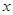
轴于点Q，若
,
.
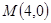(1)求点P的轨迹方程；
(2)是否存在定直线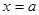
，以PM为直径的圆与直线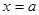的相交弦长为定值，若存在,求出定直线方程;若不存在,请说明理由。
数列{
}中，a1=3，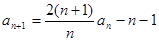
，
(1)求a1、a2、a3、a4；
(2)用合情推理猜测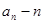
关于n的表达式(不用证明)；
(3)用合情推理猜测{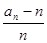
}是什么类型的数列并证明；
(4)求{}的前n项的和。
设命题p:函数
在(0，+
)上是增函数；命题q:方程
有两个不相等的负实数根，若p
q是真命题。
(1)求点P(a，b)的轨迹图形的面积；
(2)求a+5b的取值范围。