(本小题满分13 分)某厂商调查甲、乙两种不同型号电视机在10 个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.
为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)当 时,记甲型号电视机的“星级卖场”数量为
时,记甲型号电视机的“星级卖场”数量为 ,乙型号电视机的“星级卖场”数量为
,乙型号电视机的“星级卖场”数量为 ,比较
,比较 ,
, 的大小关系;
的大小关系;
(2)在这10 个卖场中,随机选取2 个卖场,记 为其中甲型号电视机的“星级卖场”的个数,求
为其中甲型号电视机的“星级卖场”的个数,求 的分布列和数学期望;
的分布列和数学期望;
(3)若 ,记乙型号电视机销售量的方差为
,记乙型号电视机销售量的方差为 ,根据茎叶图推断
,根据茎叶图推断 为何值时,
为何值时, 达到最小值.(只需写出结论)
达到最小值.(只需写出结论)
(本小题满分14分)
已知数列 的前
的前 项和为
项和为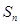 ,
,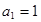 ,
, ,
,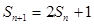 .
.
⑴求 的通项公式
的通项公式
⑵对 ,
,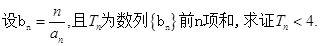
本小题满分12分)
如图,菱形 所在平面与矩形
所在平面与矩形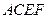 所在平面互相垂直,已知
所在平面互相垂直,已知 ,且点
,且点
 是线段
是线段 的中点.
的中点.
(l)求证: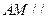

(2)求证:平面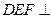 平面
平面
(本小题满分14分)已知函数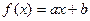 ,
, ,
,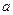 、
、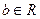 是常数.
是常数.
⑴若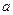 是从
是从 、
、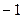 、
、 、
、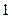 、
、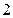 五个数中任取的一个数,
五个数中任取的一个数, 是从
是从 、
、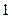 、
、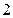 三个数中任取的一个数,求函数
三个数中任取的一个数,求函数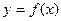 为奇函数的概率.
为奇函数的概率.
⑵若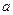 是从区间
是从区间 中任取的一个数,
中任取的一个数, 是从区间
是从区间 中任取的一个数,求函数
中任取的一个数,求函数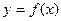 有零点的概率.
有零点的概率.
本小题满分12分)
设函数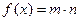 ,其中向量
,其中向量 .
.
(1)求函数 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(2)在△ 中,
中, 分别是角
分别是角 的对边,已知
的对边,已知 ,△
,△ 的面积为
的面积为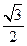 ,求△
,求△ 外接圆半径
外接圆半径 .
.
杨辉是中国南宋末年的一位杰出的数学家、数学教育家. 杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律.下图是一个11阶杨辉三角:
(1)求第20行中从左到右的第4个数;
(2)若第n行中从左到右第14与第15个数的比为 ,求n的值;
,求n的值;
(3)在第3斜列中,前5个数依次为1,3,6,10,15;第4斜列中,第5个数为35.显然,1+3+6+10+15=35.事实上,一般地有这样的结论:第m斜列中(从右上到左下)前k个数之和,一定等于第m+1斜列中第k个数.
试用含有m、k 的数学公式表示上述结论,并给予证明.
的数学公式表示上述结论,并给予证明. 