(本小题满分13 分)无穷数列  :
: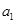 ,
,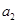 ,……,
,……, ,……,满足
,……,满足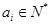 ,且
,且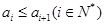 ,对于数列
,对于数列 ,记
,记 ,其中
,其中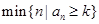 表示集合
表示集合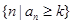 中最小的数.
中最小的数.
(1)若数列 :1,3,4,7,……,写出
:1,3,4,7,……,写出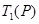 ,
,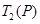 ,……,
,……,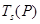 ;
;
(2)若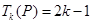 ,求数列
,求数列 前
前 项的和;
项的和;
(3)已知 ,求
,求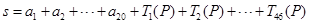 的值.
的值.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过C点,已知|AB|=3米,|AD|=2米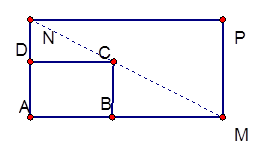
(1)要使矩形AMPN的面积大于32平方米,则AN的长度应在什么范围内?
(2)当AN的长度是多少时,矩形AMPN的面积最小?并求出最小值
设函数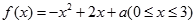 的最大值为
的最大值为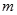 ,最小值为
,最小值为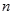 ,其中
,其中 .
.
(1)求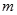 、
、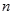 的值(用
的值(用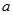 表示);
表示);
(2)已知角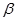 的顶点与平面直角坐标系
的顶点与平面直角坐标系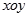 中的原点
中的原点 重合,始边与
重合,始边与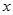 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点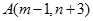 .求
.求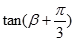 的值.
的值.
已知向量m=(2sinx,cosx),n=(cosx,2cosx),定义函数f(x)=m·n-1.
(1)求函数f(x)的最小正周期;
(2)确定函数f(x)的单调区间、对称轴与对称中心.
如图,已知抛物线 的焦点为F
的焦点为F 过点
过点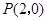 的直线交抛物线于A
的直线交抛物线于A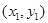 ,B
,B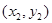 两点,直线AF,BF分别与抛物线交于点M,N
两点,直线AF,BF分别与抛物线交于点M,N 
(1)求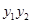 的值;
的值;
(2)记直线MN的斜率为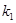 ,直线AB的斜率为
,直线AB的斜率为 证明:
证明: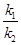 为定值
为定值
如图,三棱锥P ABC中,已知PA⊥平面ABC,△ABC是边长为2的正三角形,D,E分别为PB,PC中点 
(1)若PA=2,求直线AE与PB所成角的余弦值;
(2)若PA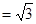 ,求证:平面ADE⊥平面PBC
,求证:平面ADE⊥平面PBC