推理填空:
如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
因为EF∥AD,
所以∠2=____(____________________________)
又因为∠1=∠2
所以∠1=∠3(______________)
所以AB∥_____(_____________________________)
所以∠BAC+______=180°
(___________________________)
因为∠BAC=70°
所以∠AGD=_______.
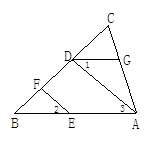
在Rt△ABC中,∠ACB=90°,AB=2AC,如图所示,求∠A、∠B的度数.
把长与宽之比为 的矩形纸片称为标准纸,请思考并解决下列问题:
的矩形纸片称为标准纸,请思考并解决下列问题:
(1)将一张标准纸ABCD(AB<BC)对开,如图1所示,所得的矩形纸片ABEF是标准纸,请给予证明;
(2)在一次综合实践课上,小明尝试着将矩形纸片ABCD(AB<BC)进行如下操作:
第一步:沿过A点的直线折叠,使B点落在AD边上点F处,折痕为AE(如图2甲);
第二步:沿过D点的直线折叠,使C点落在AD边上点N处,折痕为DG(如图2乙),此时E点恰好落在AE边上的点M处;
第三步:沿直线DM折叠(如图2丙),此时点G恰好与N点重合.
请你探究:矩形纸片ABCD是否是一张标准纸,请说明理由;
(3)不难发现:将一张标准纸按如图3所示方式一次又一次对开后,所得的矩形纸片都是标准纸,现有一张标准纸ABCD,AB=1, ,问第5次对开后所得标准纸的周长是多少?探索并直接写出第2014次对开后所得标准纸的周长.
,问第5次对开后所得标准纸的周长是多少?探索并直接写出第2014次对开后所得标准纸的周长.
如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AB=6cm,求矩形的对角线长和面积.
如图所示,在矩形ABCD中,对角线AC,BD相交于点O,∠AOD=120°,AB+AC=9,求对角线BD的长及矩形ABCD的面积.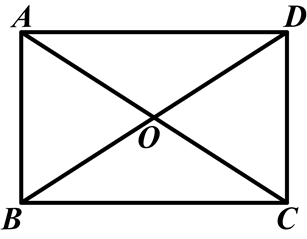
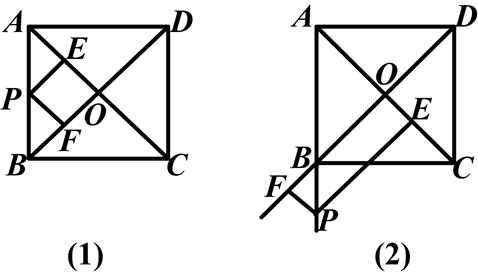
已知正方形ABCD的边长为a,两对角线相交于点O,P是射线AB上任意一点,过P点分别作直线AC、BD的垂线PE、PF,垂足为E、F.
(1)如图(1),当P在线段AB上时,求PE+PF的值.
(2)如图(2),当P在线段AB的延长线上时,求PE-PF的值.