已知椭圆 的中心在原点
的中心在原点 ,焦点在
,焦点在 轴上,离心率为
轴上,离心率为 ,右焦点到右顶点的距离为
,右焦点到右顶点的距离为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)是否存在与椭圆 交于
交于 两点的直线
两点的直线 :
: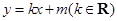 ,使得
,使得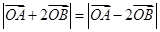 成立?若存在,求出实数
成立?若存在,求出实数 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
过点P(-3,0)且倾斜角为30°的直线和曲线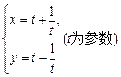 相交于A、B两点.求线段AB的长.
相交于A、B两点.求线段AB的长.
已知一四棱锥P-ABCD的三视图如下,E是侧棱PC上的动点。
(Ⅰ)求四棱锥P-ABCD的体积;
(Ⅱ)是否不论点E在何位置,都有BD⊥AE?证明你的结论;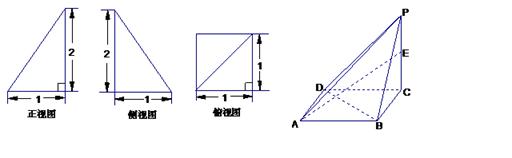
如图是一个空间几何体的三视图,其中正视图和侧视图都是边长为2的正三角形,俯视图是一个正方形.
(Ⅰ)在给定的空间直角坐标系中作出这个几何体的直观图(不用写作法);
(Ⅱ)求这个几何体的体积.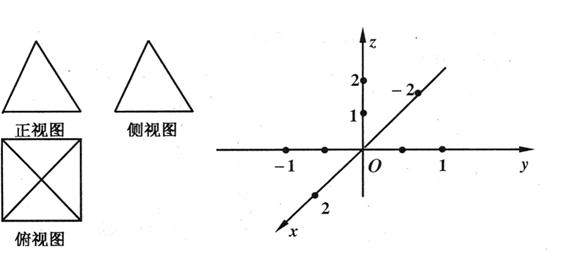
一个简单多面体的直观图和三视图如图所示,它的主视图和侧视图都是腰长为1的等腰直角三角形,俯视图为正方形,E是PD的中点.
(1)求证: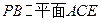 ;
;
(2)求证: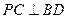 ;
;
(3)求三棱锥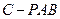 的体积.
的体积.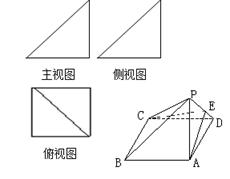
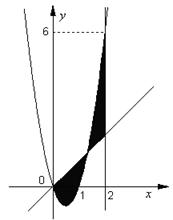
如图,已知二次函数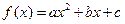 ,直线
,直线 ,直线
,直线
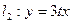 (其中
(其中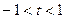 ,
,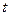 为常数);.若直线
为常数);.若直线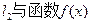 的图象以及
的图象以及 的图象所围成的封闭图形如阴影所示.
的图象所围成的封闭图形如阴影所示.
(Ⅰ)求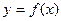 ;
;
(Ⅱ)求阴影面积s关于t的函数 的解析式;
的解析式;
(Ⅲ)若过点 可作曲线
可作曲线 的三条切线,求实数m的取值范围.
的三条切线,求实数m的取值范围.