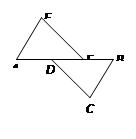列方程或方程组解应用题:
2014年北京市生产运营用水和居民家庭用水的总和为5.8亿立方米,其中居民家庭用水比生产运营用水的3倍还多0.6亿立方米,问生产运营用水和居民家庭用水各多少亿立方米.
红用下面的方法对
 进行因式分解,请你仿照他的方法分解下面另外三个二次三项式,并把你的解答过程填写在下面的表格中.
进行因式分解,请你仿照他的方法分解下面另外三个二次三项式,并把你的解答过程填写在下面的表格中.
| 方程 |
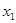 |
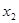 |
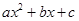 因式分解 因式分解 |
 |
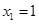 |
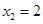 |
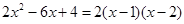 |
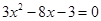 |
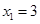 |
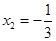 |
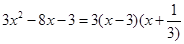 |
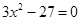 |
|||
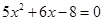 |
|||
关于x的方程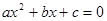 ( 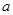 、 、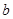 、 、 为常数, 为常数,且 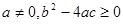 ) ) |
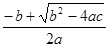 |
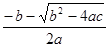 |
设
 是一元二次方程
是一元二次方程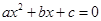
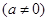 的两个实根,根据观察表格中的规律,写出二次三项式
的两个实根,根据观察表格中的规律,写出二次三项式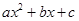
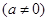 的因式分解与
的因式分解与 之间的关系式。
之间的关系式。
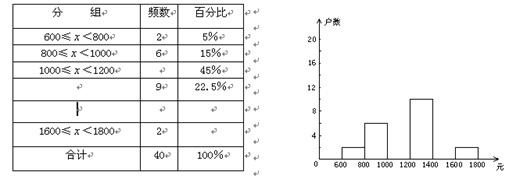
小龙在学校组织的社会调查活动中负责了解他所居住的小区600户居民的家庭收入情况. 他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图. 根据以上提供的信息,解答下列问题:补全频数分布表.
补全频数分布直方图.
请你估计该居民小区家庭属于中等收入(大于或等于1000不足1600元)的大约有多少户?
在正方形网格中,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:将△ABC向右平移5个单位长度,画出平移后的△A1B1C1 ;
画出△ABC关于x轴对称的△A2B2C2 ;
将△ABC绕原点O 旋转180°,画出旋转后的△A3B3C3 ;
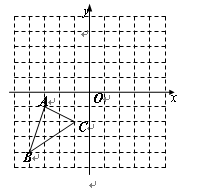
如图,反比例函数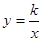 (x>0)的图象过点A 。
(x>0)的图象过点A 。
求反比例函数的解析式;
若点B在
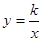 (x>0)的图象上,求直线AB的解析式.
(x>0)的图象上,求直线AB的解析式.
如图,点A、D、F、B在同一条直线上,AD=BF,AE=BC,且AE∥BC.
求证:EF∥CD