(1)利用“五点法”画出函数 在长度为一个周期的闭区间的简图
在长度为一个周期的闭区间的简图
(2)并说明该函数图象可由y=sinx(x R)的图象经过怎样平移和伸缩变换得到的。
R)的图象经过怎样平移和伸缩变换得到的。
选修4—5:不等式选讲
已知函数 ,
, ,
, .
.
(1)当 时,若
时,若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)当 时,求函数
时,求函数 的最小值.
的最小值.
选修4—4:坐标系与参数方程
极坐标系与直角坐标系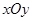 有相同的长度单位,以原点为极点,以
有相同的长度单位,以原点为极点,以 轴正半轴为极轴,曲线
轴正半轴为极轴,曲线 的极坐标方程为
的极坐标方程为 ,曲线
,曲线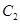 的参数方程为
的参数方程为 (
( 为参数,
为参数, ),射线
),射线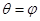 ,
, ,
, 与曲线
与曲线 交于(不包括极点
交于(不包括极点 )三点
)三点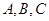 .
.
(1)求证: ;
;
(2)当 时,
时, 两点在曲线
两点在曲线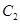 上,求
上,求 与
与 的值.
的值.
已知函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若函数 在区间
在区间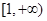 上的最小值为0,求
上的最小值为0,求 的值.
的值.
(3)若对于任意 ,
,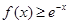 恒成立,求
恒成立,求 的取值范围.
的取值范围.
已知抛物线 的焦点为
的焦点为 ,直线
,直线 与
与 轴的交点为
轴的交点为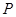 ,与抛物线
,与抛物线 的交点为
的交点为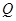 ,且
,且 .已知椭圆
.已知椭圆
 的右焦点
的右焦点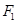 与抛物线
与抛物线 的焦点重合,且离心率为
的焦点重合,且离心率为 .
.
(1)求抛物线 和椭圆
和椭圆 的方程;
的方程;
(2)若过椭圆 的右焦点
的右焦点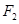 的直线
的直线 与椭圆交于
与椭圆交于 、
、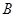 两点,求三角形
两点,求三角形 (
( 为坐标原点)的面积
为坐标原点)的面积 的最大值.
的最大值.
如图1,在 中,
中, ,
, ,
, 是
是 上的高,沿
上的高,沿 将
将 折成
折成 的二面角
的二面角 ,如图2.
,如图2.
(1)证明:平面
 平面
平面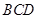 ;
;
(2)设 为
为 的中点,
的中点, ,求异面直线
,求异面直线 与
与 所成的角的大小.
所成的角的大小.