一个商场经销某种商品,根据以往资料统计,每位顾客采用的分期付款次数 的分布列为:
的分布列为:
 |
1 |
2 |
3 |
4 |
5 |
| P |
0.4 |
0.2 |
0.2 |
0.1 |
0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;采用2期或3期付款,其利润为250元;采用4期或5期付款,其利润为300元. 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(1)求购买该商品的3位顾客中,恰有2位采用1期付款的概率;
(2)求 的分布列及期望
的分布列及期望 .
.
如图, 在空间四边形SABC中, 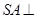 平面ABC,
平面ABC, 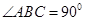 ,
, 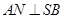 于N,
于N, 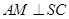 于M.
于M.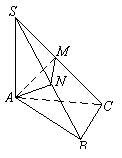
求证:①AN^BC; ②平面SAC^平面ANM
下面三个图中,右面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在左面画出(单位:cm).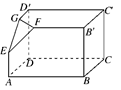
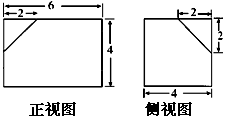
(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(2)按照给出的尺寸,求该多面体的体积;
已知圆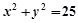 ,
, 内接于此圆,
内接于此圆,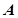 点的坐标
点的坐标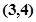 ,
, 为坐标原点.
为坐标原点.
(Ⅰ)若 的重心是
的重心是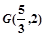 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)若直线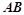 与直线
与直线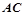 的倾斜角互补,求证:直线
的倾斜角互补,求证:直线 的斜率为定值.
的斜率为定值.
如图,AB是过椭圆左焦点F的一弦,C是椭圆的右焦点,已知|AB|=|AC|=4,∠BAC=90°,求椭圆方程.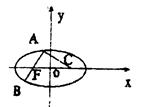
求与双曲线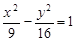 有共同渐近线,并且经过点 (-3,
有共同渐近线,并且经过点 (-3, )的双曲线方程.
)的双曲线方程.