(本小题满分13分)已知A、B、C是三角形的内角, sin A,-cos A是方程x2-x+2a=0的两根.
sin A,-cos A是方程x2-x+2a=0的两根.
(1)求角A;
(2)若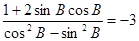 ,求tan B.
,求tan B.
(本小题满分 分)
分)
在四棱锥 中,平面
中,平面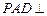 平面
平面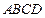 ,△
,△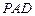 是等边三角形,底面
是等边三角形,底面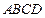 是边长为
是边长为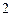 的菱形,
的菱形, ,
,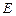 是
是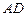 的中点,
的中点,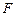 是
是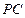 的中点.
的中点.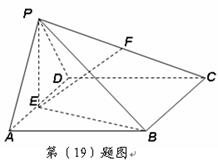
(Ⅰ)求证: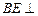 平面
平面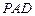 ;
;
(Ⅱ) 求证: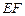 ∥平面
∥平面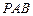 ;
;
(Ⅲ) 求直线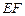 与平面
与平面 所成角的余弦值.
所成角的余弦值.
(本小题满分 分)某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.
分)某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.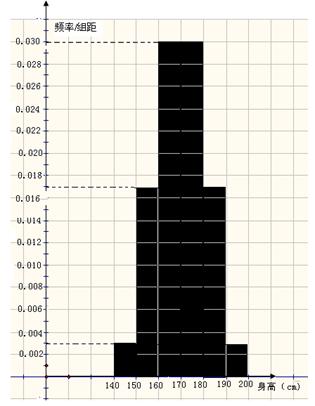
(Ⅰ)求甲、乙两同学都被抽到的概率,其中甲为A类同学,乙为B类同学;
(Ⅱ) 测得该年级所抽查的100名同学身高(单位:厘米) 频率分布直方图如右图:
(ⅰ) 统计方法中,同一组数据常用该组区间的中点值(例如区间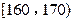 的中点值为165)作为代表.据此,计算这100名学生身高数据的期望
的中点值为165)作为代表.据此,计算这100名学生身高数据的期望 及标准差
及标准差 (精确到0.1);
(精确到0.1);
(ⅱ) 若总体服从正态分布,以样本估计总体,据此,估计该年级身高在 范围中的学生的人数.
范围中的学生的人数.
(Ⅲ) 如果以身高达170cm作为达标的标准,对抽取的100名学生,得到下列联表:
体育锻炼与身高达标2×2列联表
| 身高达标 |
身高不达标 |
总计 |
|
| 积极参加体育锻炼 |
40 |
||
| 不积极参加体育锻炼 |
15 |
||
| 总计 |
100 |
(ⅰ)完成上表;
(ⅱ)请问有多大的把握认为体育锻炼与身高达标有关系?
参考公式:K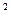 =
=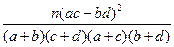 ,参考数据:
,参考数据:
P(K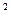 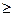 k) k) |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
| k |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
(本小题满分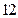 分)设数列
分)设数列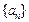 的前
的前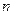 项和为
项和为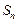 ,且
,且 ,
,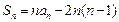 .
.
(Ⅰ)求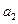 ,
,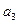 ,
, ,并求出数列
,并求出数列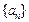 的通项公式;
的通项公式;
(Ⅱ)设数列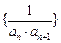 的前
的前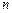 项和为
项和为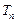 ,试求
,试求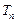 的取值范围.
的取值范围.
(满分12分)直线l 与抛物线y2 = 4x 交于两点A、B,O 为原点,且 = -4.
= -4.
(I)求证:直线l 恒过一定点;
(II)若 4 ≤| AB | ≤
≤| AB | ≤ ,求直线l 的
,求直线l 的 斜率k 的取值范围;
斜率k 的取值范围;
(Ⅲ) 设抛物线的焦点为F,∠AFB = θ,试问θ 角 能否
能否 等于120°?若能,求出相应的直线l 的方程;若不能,请说明理由.
等于120°?若能,求出相应的直线l 的方程;若不能,请说明理由.
(满分12分)设f (x) 是定义在 [-1,1] 上的偶函数,f (x) 与g(x) 的图象关于x =" 1" 对称,且当x Î [2,3] 时,g(x) = a (x-2)-2 (x-2) 3(a 为常数). (Ⅰ)求f (x) 的解析式;
(Ⅰ)求f (x) 的解析式;
(Ⅱ)若f (x) 在 [0,1] 上是增函数,求实数a 的取值范围;
(Ⅲ)若a  Î (-6,6),问能否使f (x) 的最大值为 4?请说明理由.
Î (-6,6),问能否使f (x) 的最大值为 4?请说明理由.