(本小题满分12分)已知函数 .
.
(1)判断 的奇偶性.
的奇偶性.
(2)判断 在
在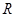 上的单调性,并用定义证明.
上的单调性,并用定义证明.
(3)是否存在实数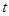 ,使不等式
,使不等式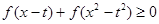 对一切
对一切 恒成立?若存在,求出
恒成立?若存在,求出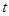 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
甲、乙等五名亚运志愿者被随机地分到 四个不同的赛场服务,每个赛场至少有一名志愿者。
四个不同的赛场服务,每个赛场至少有一名志愿者。
(Ⅰ)求甲、乙两人同时参加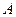 赛场服务的概率;
赛场服务的概率;
(Ⅱ)求甲、乙两人不在同一个赛场服务的概率;
(Ⅲ)设随机变量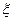 为这五名志愿者中参加
为这五名志愿者中参加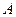 赛场服务的人数,求
赛场服务的人数,求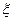 的分布列。
的分布列。
在数列 中,
中, ,
, ,且
,且 (
(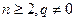 )。
)。
(Ⅰ)设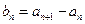 (
( ),求数列
),求数列 的通项公式;
的通项公式;
(Ⅱ)求数列 的通项公式。
的通项公式。
设函数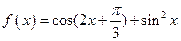 。
。
(Ⅰ)求函数 的最小正周期,并判断奇偶性;
的最小正周期,并判断奇偶性;
(Ⅱ)设A,B,C为 的三个内角,若
的三个内角,若 ,且C为锐角,求
,且C为锐角,求 。
。
已知函数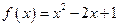 设计一个算法步骤求
设计一个算法步骤求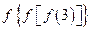 的值.
的值.
规定A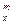 =x(x-1)…(x-m+1),其中x∈R,m为正整数,且A
=x(x-1)…(x-m+1),其中x∈R,m为正整数,且A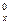 =1,这是排列数A
=1,这是排列数A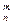 (n,m是正整数,且m≤n)的一种推广.
(n,m是正整数,且m≤n)的一种推广.
(1)求A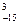 的值;
的值;
(2)排列数的两个性质:①A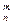 =nA
=nA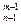 ,②A
,②A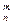 +mA
+mA =A
=A (其中m,n是正整数).是否都能推广到A
(其中m,n是正整数).是否都能推广到A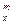 (x∈R,m是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
(x∈R,m是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
(3)确定函数A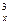 的单调区间.
的单调区间.