(本小题满分14分)已知函数 (a∈R).
(a∈R).
(Ⅰ)若函数 为偶函数,求
为偶函数,求 的值;
的值;
(Ⅱ)当
 时,若对任意的
时,若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题12分)在平面直角坐标系中,已知一个椭圆的中心在原点,左焦点为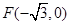 ,且过
,且过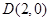 .
.
(1)求该椭圆的标准方程;
(2)若 是椭圆上的动点,点
是椭圆上的动点,点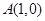 ,求线段
,求线段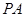 中点
中点 的轨迹方程.
的轨迹方程.
(本小题12分)已知某校高二文科班学生的化学与物理的水平测试成绩抽样统计如下表,若抽取学生n人,成绩分为A(优秀)、B(良好)、C(及格)三个等级,设x,y分别表示化学成绩与物理成绩.例如:表中化学成绩为B等级的共有20+18+4=42人,已知x与y均为B等级的概率是0.18.
| x 人数 y |
A |
B |
C |
| A |
7 |
20 |
5 |
| B |
9 |
18 |
6 |
| C |
a |
4 |
b |
(1)求抽取的学生人数;
(2)设该样本中,化学成绩优秀率是30%,求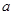 ,
,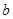 值;
值;
(3)在物理成绩为C等级的学生中,已知a≥10,b≥8,求化学成绩为A等级的人数比C等级的人数少的概率.
(本小题12分)设有关于x的一元二次方程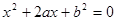 .
.
(1)若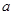 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数,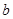 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
(2)若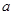 是从区间
是从区间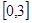 任取得一个数,
任取得一个数,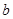 是从区间
是从区间 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
(本小题12分)某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.
| 分数段 |
[50,60) |
[60,70) |
[70,80) |
[80,90) |
| x∶y |
1∶1 |
2∶1 |
3∶4 |
4∶5 |
(本小题10分)对甲、乙的学习成绩进行抽样分析,各抽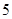 门功课,得到的观测值如表,问:
门功课,得到的观测值如表,问:
甲、乙谁的平均成绩最好?谁的各门功课发展较平衡?