在如图所示的几何体中，四边形
是菱形，
是矩形，平面⊥平面，
是
的中点．
（1）求证：
∥平面
；
（2）在线段
上是否存在点
，使二面角
的大小为
？若存在，求出
的长；若不存在，请说明理由．
（本小题满分12分）已知函数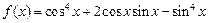
.
（1）求
的递减区间；
（2）当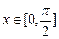
时，求的最小值以及取得最小值时
的集合.
（本题12分）已知关于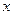
的不等式
，其中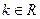
.
（Ⅰ）当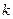
变化时，试求不等式的解集
；
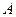（Ⅱ）对于不等式的解集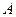，若满足
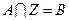（其中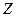
为整数集）. 试探究集合
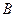能否为有限集？若能，求出使得集合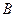中元素个数最少的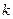的所有取值，并用列举法表示集合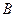；若不能，请说明理由.
（本题10分）上海“世博会”举办时间为2010年5月1日～10月31日．陕西馆以“人文长安之旅”为主题，以“昔日皇家园林”华清池为原型，塑造“人文陕西、山水秦岭”的新形象．为宣传陕西，要设计如图的一张矩形广告，该广告含有大小相等的左中右三个矩形栏目，这三栏的面积之和为
，四周空白的宽度为
，栏与栏之间的中缝空白的宽度为
，怎样确定广告矩形栏目高与宽的尺寸(单位：
)，能使整个矩形广告面积最小.
（本题10分）已知
，求证：
（本题8分）解不等式